【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.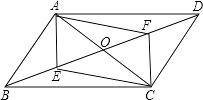
(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵点E、F分别为BO、DO的中点,
∴EO=OF,
∵AO=CO,
∴四边形AECF是平行四边形;
(2)解:结论仍然成立,
理由:∵BE=DF,BO=DO,
∴EO=FO,
∵AO=CO,
∴四边形AECF是平行四边形.
【解析】(1)由平行四边形ABCD,得出对角线互相平分即AO=CO,BO=DO,再根据点E、F分别为BO、DO的中点,可证得EO=OF,根据对角线互相平分的四边形是平行四边形,即可得证。
(2)E,F点分别在DB和BD的延长线上时,且满足BE=DF,结论仍然成立,证法同(1)。
【考点精析】认真审题,首先需要了解平行四边形的判定与性质(若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积).
-
科目: 来源: 题型:
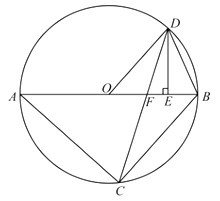
查看答案和解析>>【题目】如图,已知
 内接于
内接于  ,
,  是直径,点
是直径,点  在
在  上,
上, 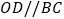 ,过点
,过点  作
作  ,垂足为
,垂足为  ,连接
,连接 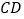 交
交 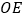 边于点
边于点 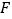 .
.
(1)求证: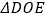 ∽
∽ 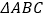 ;
;
(2)求证: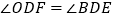 ;
;
(3)连接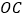 ,设
,设 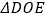 的面积为
的面积为 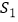 ,四边形
,四边形 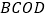 的面积为
的面积为 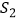 ,若
,若 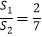 ,求
,求 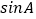 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A.
 B.
B.  C. 3 D.
C. 3 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为预防甲型H1N1流感,某校对教室喷洒药物进行消毒.已知喷洒药物时每立方米空气中的含药量y(毫克)与时间x(分钟)成正比,药物喷洒完后,y与x成反比例(如图所示).现测得10分钟喷洒完后,空气中每立方米的含药量为8毫克.
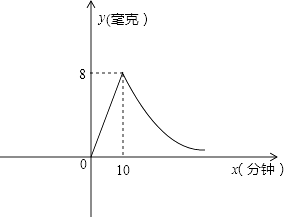
(1)求喷洒药物时和喷洒完后,y关于x的函数关系式;
(2)若空气中每立方米的含药量低于2毫克学生方可进教室,问消毒开始后至少要经过多少分钟,学生才能回到教室?
(3)如果空气中每立方米的含药量不低于4毫克,且持续时间不低于10分钟时,才能杀灭流感病毒,那么此次消毒是否有效?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接一个对角线互相垂直的四边形各边中点,所得的四边形是 形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“直角”在初中几何学习中无处不在. 如图,已知∠AOB,请仿照小丽的方式,再用两种不同的方法判断∠AOB是否为直角(仅限用直尺和圆规).
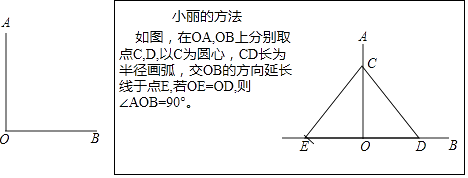
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道多项式的乘法可以利用图形的面积进行解释,例如,(2a+b)(a+b)=2a2+3ab+b2就能用图1或图2等图形的面积表示:
(1)请你写出图3所表示的一个等式: .
(2)试画出一个图形,使它的面积能表示成(a+b)(a+3b)=a2+4ab+3b2.
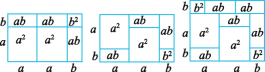
图1 图2 图3
相关试题

