【题目】我们知道多项式的乘法可以利用图形的面积进行解释,例如,(2a+b)(a+b)=2a2+3ab+b2就能用图1或图2等图形的面积表示:
(1)请你写出图3所表示的一个等式: .
(2)试画出一个图形,使它的面积能表示成(a+b)(a+3b)=a2+4ab+3b2.
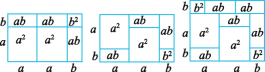
图1 图2 图3
参考答案:
【答案】(1)(a+2b)(2a+b)=2a2+5ab+2b2 (2)见解析
【解析】
试题(1)由题意得:长方形的面积=长×宽,即可将长和宽的表达式代入,再进行多项式的乘法,即可得出等式;
(2)已知图形面积的表达式,即可根据表达式得出图形的长和宽的表达式,即可画出图形.
解:(1)∵长方形的面积=长×宽,
∴图3的面积=(a+2b)(2a+b)=2a2+5ab+2b2,
故图3所表示的一个等式:(a+2b)(2a+b)=2a2+5ab+2b2,
故答案为:(a+2b)(2a+b)=2a2+5ab+2b2;
(2)∵图形面积为:(a+b)(a+3b)=a2+4ab+3b2,
∴长方形的面积=长×宽=(a+b)(a+3b),
由此可画出的图形为:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.
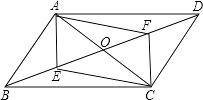
(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接一个对角线互相垂直的四边形各边中点,所得的四边形是 形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“直角”在初中几何学习中无处不在. 如图,已知∠AOB,请仿照小丽的方式,再用两种不同的方法判断∠AOB是否为直角(仅限用直尺和圆规).
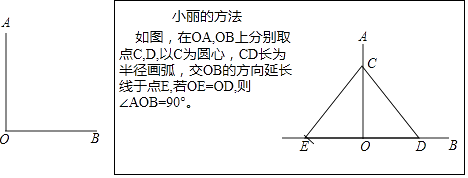
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.

A. ① B. ①② C. ①②③ D. 都不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中点,AB=
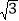 ,AD=2,BC=3,下列结论:
,AD=2,BC=3,下列结论:①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD.

(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
相关试题

