【题目】古希腊数学家丢番图(公元3~4世纪)的墓碑上记栽着:“他生命的六分之一是幸福的童年;再活了他生命的十二分之一,两颊长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他有了儿子,感到很幸福;可是儿子只活了他父亲全部年龄的一半;儿子死后,他在极度悲痛中度过了四年,也与世长辞了.”根据以上信息,请你算出:
(1)丢番图的寿命;
(2)丢番图开始当爸爸时的年龄;
(3)儿子死时丢番图的年龄.
参考答案:
【答案】
(1)解:设丢番图的寿命为x岁,
由题意得: ![]() x+
x+ ![]() x+
x+ ![]() x+5+
x+5+ ![]() x+4=x,
x+4=x,
解得:x=84
(2)解:而 ![]() ×84+
×84+ ![]() ×84+
×84+ ![]() ×84+5=38,即他38岁时有了儿子
×84+5=38,即他38岁时有了儿子
(3)解:他儿子活了 ![]() x=42岁.
x=42岁.
84﹣4=80岁
【解析】设丢番图的寿命为x岁,则根据题中的描述他的年龄= ![]() x的童年+生命的
x的童年+生命的 ![]() x+
x+ ![]() x+5年+儿子的年龄+4年,可列出方程,即可求解.
x+5年+儿子的年龄+4年,可列出方程,即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=x+1的图像不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-
 x+4与x轴交于点A,与y交于点C,已知二次函数的图象经过点A,C和点B(-1,0),
x+4与x轴交于点A,与y交于点C,已知二次函数的图象经过点A,C和点B(-1,0),(1)求该二次函数的关系式;
(2)设该二次函数的图象的顶点为M,求四边形AOCM的面积;
(3)有两个动点D、E同时从点O出发,其中点D以每秒
 个单位长度的速度沿折线OAC按O→A→C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O→C→A的路线运动,当点D、E两点相遇时,它们都停止运动,设D,E同时从点O出发t秒时,△ODE的面积为S,
个单位长度的速度沿折线OAC按O→A→C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O→C→A的路线运动,当点D、E两点相遇时,它们都停止运动,设D,E同时从点O出发t秒时,△ODE的面积为S,
①请问D,E两点在运动过程中,是否存在DE∥OC,若存在,请求出此时t的值,若不存在,请说明理由;
②直接写出S关于t的函数关系式,并写出自变量t的取值范围;
③在②中,当t是多少时,S有最大值,并求出这个最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据测试,拧不紧的水龙头每秒会滴下2滴水,每滴水约0.05毫升,小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后水龙头滴下的水用科学记数法表示为毫升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了5
 km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点. 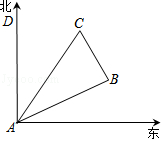
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A,B,C分别表示有理数a ,b ,c,若ac<0, a+b>0,则原点位于( )

A.点A的左侧
B.点A与点B之间
C.点B与点C之间
D.在点C的右侧 -
科目: 来源: 题型:
查看答案和解析>>【题目】若x=0是关于x的一元二次方程(m﹣2)x2+3x+m2+2m﹣8=0的一个解,求实数m的值和另一个根.
相关试题

