【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() .点
.点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的表达式;
的表达式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,
的位置,![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.

参考答案:
【答案】(1)C(-13,0),E(-5,-3),![]() ;(2)32;(3)见解析.
;(2)32;(3)见解析.
【解析】
(1)利用坐标轴上点的特点确定出点C的坐标,再利用直线的交点坐标的确定方法求出点E坐标,进而得到点B坐标,最后用待定系数法求出直线AB解析式;
(2)直接利用直角三角形的面积计算方法和直角梯形的面积的计算即可得出结论,
(3)先求出直线AB与x轴的交点坐标,判断出点C不在直线AB上,即可.
(1)在直线![]() 中,令y=0,则有0=
中,令y=0,则有0=![]() ,
,
∴x=﹣13,
∴C(﹣13,0),
令x=﹣5,代入![]() ,解得y=﹣3,
,解得y=﹣3,
∴E(﹣5,﹣3),
∵点B,E关于x轴对称,
∴B(﹣5,3),
∵A(0,5),
∴设直线AB的解析式为y=kx+5,
∴﹣5k+5=3,
∴k=![]() ,
,
∴直线AB的解析式为![]() ;
;
(2)由(1)知E(﹣5,﹣3),
∴DE=3,
∵C(﹣13,0),
∴CD=﹣5﹣(﹣13)=8,
∴S△CDE=![]() CD×DE=12,
CD×DE=12,
由题意知,OA=5,OD=5,BD=3,
∴S四边形ABDO=![]() (BD+OA)×OD=20,
(BD+OA)×OD=20,
∴S=S△CDE+S四边形ABDO=12+20=32;
(3)由(2)知,S=32,
在△AOC中,OA=5,OC=13,
∴S△AOC=![]() OA×OC=
OA×OC=![]() =32.5,
=32.5,
∴S≠S△AOC,
理由:由(1)知,直线AB的解析式为![]() ,令y=0,则0=
,令y=0,则0=![]() ,
,
∴x=﹣![]() ≠﹣13,
≠﹣13,
∴点C不在直线AB上,
即:点A,B,C不在同一条直线上,
∴S△AOC≠S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )

A.42°
B.28°
C.21°
D.20° -
科目: 来源: 题型:
查看答案和解析>>【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和
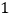 个过滤网要花费
个过滤网要花费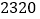 元,买
元,买 个空气净化器和
个空气净化器和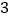 个过滤网要花费
个过滤网要花费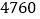 元.
元.(
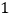 )请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?(
 )为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买
)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买 个空气净化器和
个空气净化器和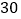 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,则水的最大深度CD为( )

A.4cm
B.3cm
C.2cm
D.1cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,以
,以 长为一边作
长为一边作 ,
, ,取
,取 中点
中点 ,连
,连 、
、 、
、 .
. 求证:
求证:
 当
当 ________时,
________时, 是等边三角形,并说明理由.
是等边三角形,并说明理由. 当
当 时,若
时,若 ,取
,取 中点
中点 ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )
A.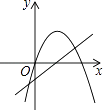
B.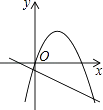
C.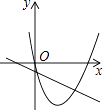
D.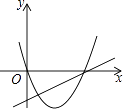
-
科目: 来源: 题型:
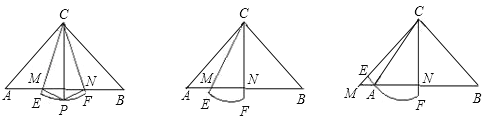
查看答案和解析>>【题目】已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.
(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是 .线段AM、BN、MN之间的数量关系是 ;
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是 .试证明你的猜想;
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是 .(不要求证明)
相关试题

