【题目】(1)解方程:![]()
(2)已知关于![]() 的方程
的方程 ![]() 的解是正数,求
的解是正数,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)x= -![]() (2)m>-6且m≠-4
(2)m>-6且m≠-4
【解析】
(1)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论;
(2) 首先去分母,化成整式方程,求得x的值,然后根据方程的解大于0,且x-2≠0即可求得m的范围.
解:(1)![]() 1=
1=![]()
两边都乘(x+2)(x2),得
x(x+2)(x+2)(x2)=1,
解得x=![]() ,
,
检验:当x=![]() 时,(x+2)(x2)=
时,(x+2)(x2)=![]() ≠0,
≠0,
∴原分式方程的解为x=![]() ;
;
(2)![]() =3
=3
去分母,得2x+m=3(x2),
去括号,得2x+m=3x6,
解得:x=m+6,
根据题意得:m+62≠0且m+6>0,
解得:m>6且m≠4.
故答案是:(1) x=![]() ;(2)m>6且m≠4.
;(2)m>6且m≠4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接五一国际劳动节,某校团委组织了“劳动最光荣”有奖征文活动,并设立了一、二、三等奖.学校计划派人根据设奖情况买50件奖品,其中二等奖件数比一等奖件数的2倍还少10件,三等奖所花钱数不超过二等奖所花钱数的1.5倍.各种奖品的单价如下表所示.如果计划一等奖买x件,买50件奖品的总钱数是w元.
(1)求w与x的函数关系式及自变量
 的取值范围;
的取值范围;(2)请你计算一下,如何购买这三种奖品所花的总钱数最少?最少是多少元?
一等奖
二等奖
三等奖
12元
10元
5元
-
科目: 来源: 题型:
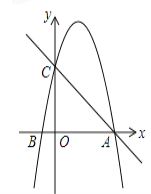
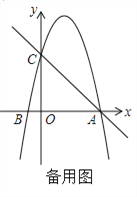
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A 的坐标是(4,0),并且0A=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1) 求抛物线的解析式;
(2)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标;
(3) 是否存在点P,使得△ACP是以AC为直角边的直角三角形? 若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组)或方程(组):
(1)
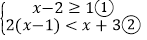 (2)
(2)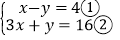
(3)(x-5)(x+4)=10;(4)
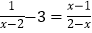 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于
 的方程2x2+kx-1=0 .
的方程2x2+kx-1=0 .(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是-1,求另一个根及k值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】供电局的电力维修工甲、乙两人要到30千米远的A地进行电力抢修.甲骑摩托车先行,
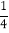 小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.(1)设摩托车的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.
(要求:填上适当的代数式,完成表格)
速度(千米/时)
所走的路程(千米)
所用时间(时)
摩托车
x
30
抢修车
30
(2)列出方程,并求摩托车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索:在图1至图2中,已知
 的面积为a
的面积为a
(1)如图1,延长
 的边BC到点D,使CD=BC,连接DA;延长边CA到点E,使CA=AE,连接DE;若
的边BC到点D,使CD=BC,连接DA;延长边CA到点E,使CA=AE,连接DE;若 的面积为
的面积为 ,则
,则 = (用含a的代数式表示);
= (用含a的代数式表示);(2)在图1的基础上延长AB到点F,使BF=AB,连接FD,FE,得到
 (如图2).若阴影部分的面积为
(如图2).若阴影部分的面积为 ,则
,则 = (用a含的代数式表示);
= (用a含的代数式表示);(3)发现:像上面那样,将
 各边均顺次延长一倍,连接所得端点,得到
各边均顺次延长一倍,连接所得端点,得到 (如图2),此时,我们称
(如图2),此时,我们称 向外扩展了一次.可以发现,扩展n次后得到的三角形的面积是
向外扩展了一次.可以发现,扩展n次后得到的三角形的面积是 面积的 倍(用含n的代数式表示);
面积的 倍(用含n的代数式表示);(4)应用:某市准备在市民广场一块足够大的空地上栽种牡丹花卉,工程人员进行了如下的图案设计:首先在
 的空地上种紫色牡丹,然后将
的空地上种紫色牡丹,然后将 向外扩展二次(如图3).在第一次扩展区域内种黄色牡丹,第二次扩展区域内种紫色牡丹,紫色牡丹花的种植成本为100元/平方米,黄色牡丹花的种植成本为95元/平方米.要使得种植费用不超过48700元,工程人员在设计时,三角形
向外扩展二次(如图3).在第一次扩展区域内种黄色牡丹,第二次扩展区域内种紫色牡丹,紫色牡丹花的种植成本为100元/平方米,黄色牡丹花的种植成本为95元/平方米.要使得种植费用不超过48700元,工程人员在设计时,三角形 的面积至多为多少平方米?
的面积至多为多少平方米?
相关试题

