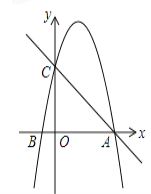
【题目】如图,在平面直角坐标系中,已知点A 的坐标是(4,0),并且0A=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1) 求抛物线的解析式;
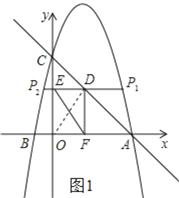
(2)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标;
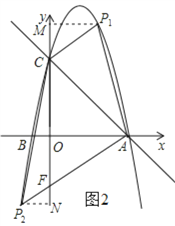
(3) 是否存在点P,使得△ACP是以AC为直角边的直角三角形? 若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由
参考答案:
【答案】(1) y=-x2+3x+4;(2)P(![]() ,2)或(
,2)或(![]() ,2);(3)存在,P的坐标是(2,6)或(-2,-6),理由见解析
,2);(3)存在,P的坐标是(2,6)或(-2,-6),理由见解析
【解析】试题分析:
(1)由已知条件易得点ABC三点的坐标,设抛物线的解析式为![]() ,将三点坐标代入所设解析式列出方程组,解方程组即可;
,将三点坐标代入所设解析式列出方程组,解方程组即可;
(2)如图1,连接OD,易证四边形OFDE是矩形,由此可得EF=OD,所以当OD最短时,EF最短,即当OD⊥AC时,EF最短,结合OA=OC可知此时点D是AC中点,从而可得点D的纵坐标,结合DF∥OC可得点P的纵坐标,代入抛物线解析式即可求得点P的横坐标,从而可得点P的坐标;
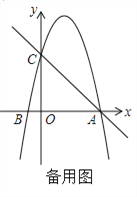
(3)如图2,根据题意分别过点A、C作AC的垂线与抛物线相交于点P,再分别过所得点P向y轴作垂线交y轴于一点,结合已知条件即可求出对应的点P的坐标了.
试题解析:
(1)∵点A的坐标为:(4,0),
∴OA=4,
∵OA=OC=4OB,
∴OA=OC=4,OB=1,
∴C(0,4),B(-1,0)
设抛物线的解析式是y=ax2+bx+c,
则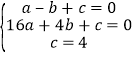 ,解得:
,解得: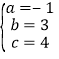 ,
,
∴抛物线的解析式是:y=-x2+3x+4;
(2)如图1,连接OD,由题意可知,四边形OFDE是矩形,
则OD=EF.根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短.
∵OA=OC,点OD⊥AC,
∴D是AC的中点.
又∵DF∥OC,
∴DF=![]() OC=2,
OC=2,
∴点P的纵坐标是2.则-x2+3x+4=2,解得:x=![]() ,
,
∴当EF最短时,点P的坐标是:(![]() ,2)或(
,2)或(![]() ,2).
,2).
(3)存在,如图2,
第一种情况,当以C为直角顶点时,过点C作CP1⊥AC,交抛物线于点P1.过点P1作y轴的垂线,垂足是M.
∵∠ACP1=90°,
∴∠MCP1+∠ACO=90°.
∵∠ACO+∠OAC=90°,
∴∠MCP1=∠OAC.
∵OA=OC,
∴∠MCP1=∠OAC=45°,
∴∠MCP1=∠MP1C,∴MC=MP1,
设P(m,-m2+3m+4),则m=-m2+3m+4-4,解得:m1=0(舍去),m2=2.
∴-m2+3m+4=6,
即P(2,6);
第二种情况,当点A为直角顶点时,过A作AP2,AC交抛物线于点P2,过点P2作y轴的垂线,垂足是N,AP交y轴于点F.
∴P2N∥x轴,由∠CAO=45°,
∴∠OAP=45°,
∴∠FP2N=45°,AO=OF.
∴P2N=NF,
设P2(n,-n2+3n+4),则n=(-n2+3n+4)+4,解得:n1=-2,n2=4(舍去),
∴-n2+3n+4=-6,则P2的坐标是(-2,-6).
综上所述,P的坐标是(2,6)或(-2,-6);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.

-
科目: 来源: 题型:
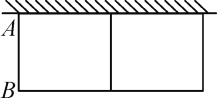
查看答案和解析>>【题目】如图,为了美化街道,刘大爷准备利用自家墙外的空地种植两种不同的花卉,墙的最大可用长度是12.5m,墙外可用宽度为3.25m.现有长为21m的篱笆,计划靠着院墙围成一个中间有一道隔栏的长方形花圃.
(1)若要围成总面积为36m2的花圃,边AB的长应是多少?
(2)花圃的面积能否达到36.75m2?若能,求出边AB的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接五一国际劳动节,某校团委组织了“劳动最光荣”有奖征文活动,并设立了一、二、三等奖.学校计划派人根据设奖情况买50件奖品,其中二等奖件数比一等奖件数的2倍还少10件,三等奖所花钱数不超过二等奖所花钱数的1.5倍.各种奖品的单价如下表所示.如果计划一等奖买x件,买50件奖品的总钱数是w元.
(1)求w与x的函数关系式及自变量
 的取值范围;
的取值范围;(2)请你计算一下,如何购买这三种奖品所花的总钱数最少?最少是多少元?
一等奖
二等奖
三等奖
12元
10元
5元
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组)或方程(组):
(1)
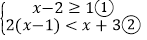 (2)
(2)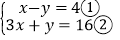
(3)(x-5)(x+4)=10;(4)
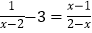 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:
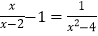
(2)已知关于
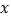 的方程
的方程 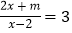 的解是正数,求
的解是正数,求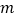 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于
 的方程2x2+kx-1=0 .
的方程2x2+kx-1=0 .(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是-1,求另一个根及k值.
相关试题

