【题目】供电局的电力维修工甲、乙两人要到30千米远的A地进行电力抢修.甲骑摩托车先行,![]() 小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
(1)设摩托车的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.
(要求:填上适当的代数式,完成表格)
速度(千米/时) | 所走的路程(千米) | 所用时间(时) | |
摩托车 | x | 30 | |
抢修车 | 30 |
(2)列出方程,并求摩托车的速度.
参考答案:
【答案】(1)摩托车的时间![]() ,抢修车的速度1.5x,时间
,抢修车的速度1.5x,时间![]() (2)40千米/时
(2)40千米/时
【解析】
(1)设摩托车的速度为x千米/时,根据时间=路程÷速度,可填写表格.
(2)设摩托车的速度为x千米/时,根据电力维修工甲、乙两人要到30千米远的A地进行电力抢修.甲骑摩托车先行,![]() 小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,可列方程求解.
小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,可列方程求解.
解:(1)设摩托车的速度为x千米/时,
速度(千米/时) | 所走的路程(千米) | 所用时间(时) | |
摩托车 | x | 30 |
|
抢修车 | 1.5x | 30 |
|
(2)设摩托车的速度为x千米/时,
由题意得![]()
![]() =
=![]() ,
,
解得x=40,
经检验,x=40是原方程的解且符合题意.
答:摩托车的速度为40千米/时.
故答案为:(1) ![]() ,1.5x,
,1.5x,![]() ;(2) 40千米/时.
;(2) 40千米/时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组)或方程(组):
(1)
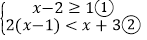 (2)
(2)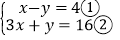
(3)(x-5)(x+4)=10;(4)
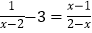 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:
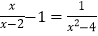
(2)已知关于
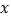 的方程
的方程 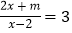 的解是正数,求
的解是正数,求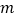 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于
 的方程2x2+kx-1=0 .
的方程2x2+kx-1=0 .(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是-1,求另一个根及k值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索:在图1至图2中,已知
 的面积为a
的面积为a
(1)如图1,延长
 的边BC到点D,使CD=BC,连接DA;延长边CA到点E,使CA=AE,连接DE;若
的边BC到点D,使CD=BC,连接DA;延长边CA到点E,使CA=AE,连接DE;若 的面积为
的面积为 ,则
,则 = (用含a的代数式表示);
= (用含a的代数式表示);(2)在图1的基础上延长AB到点F,使BF=AB,连接FD,FE,得到
 (如图2).若阴影部分的面积为
(如图2).若阴影部分的面积为 ,则
,则 = (用a含的代数式表示);
= (用a含的代数式表示);(3)发现:像上面那样,将
 各边均顺次延长一倍,连接所得端点,得到
各边均顺次延长一倍,连接所得端点,得到 (如图2),此时,我们称
(如图2),此时,我们称 向外扩展了一次.可以发现,扩展n次后得到的三角形的面积是
向外扩展了一次.可以发现,扩展n次后得到的三角形的面积是 面积的 倍(用含n的代数式表示);
面积的 倍(用含n的代数式表示);(4)应用:某市准备在市民广场一块足够大的空地上栽种牡丹花卉,工程人员进行了如下的图案设计:首先在
 的空地上种紫色牡丹,然后将
的空地上种紫色牡丹,然后将 向外扩展二次(如图3).在第一次扩展区域内种黄色牡丹,第二次扩展区域内种紫色牡丹,紫色牡丹花的种植成本为100元/平方米,黄色牡丹花的种植成本为95元/平方米.要使得种植费用不超过48700元,工程人员在设计时,三角形
向外扩展二次(如图3).在第一次扩展区域内种黄色牡丹,第二次扩展区域内种紫色牡丹,紫色牡丹花的种植成本为100元/平方米,黄色牡丹花的种植成本为95元/平方米.要使得种植费用不超过48700元,工程人员在设计时,三角形 的面积至多为多少平方米?
的面积至多为多少平方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F分别是AD和BC上的两点,EF将四边形ABCD分成两个边长为5cm的正方形,∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm,点P从点H出发,沿HD以lcm/s的速度运动,同时点Q从点A出发,沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.

(1)如图1,点Q在AB上运动,连结QF,当t= 时,QF//EP;
(2)如图2,若QE⊥EP,求出t的值;
(3)试探究:当t为何值时,
 的面积等于
的面积等于 面积的
面积的 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p,x1·x2=q.请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0 (n≠0),求出一个一元二次方程,使它的两根分别是已知方程两根的倒数;
(2)已知a、b满足a2-15a-5=0,b2-15b-5=0,求
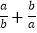 的值;
的值;(3)已知a、b、c均为实数,且a+b+c=0,abc=16,求正数c的最小值.
相关试题

