【题目】如图,已知:AD平分∠CAE,AD∥BC.
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论.

参考答案:
【答案】(1)证明见解析;(2)当∠CAE=120°时,△ABC是等边三角形,证明见解析.
【解析】试题分析:
(1)由已知条件易得∠EAD=∠CAD,∠EAD=∠B,∠CAD=∠C,从而可得∠B=∠C,进一步可得AB=AC,由此即可得到△ABC是等腰三角形;
(2)由(1)可知△ABC是等腰三角形,因此当∠BAC=60°,即∠CAE=120°时,△ABC是等边三角形.
试题解析:
(1)∵AD平分∠CAE,
∴∠EAD=∠CAD,
∵AD∥BC,
∴∠EAD=∠B,∠CAD=∠C,
∴∠B=∠C,
∴AB=AC.
故△ABC是等腰三角形.
(2)当∠CAE=120°时,△ABC是等边三角形,理由如下:
∵∠CAE=120°,
∴∠BAC=180°-∠CAE=180°-120°=60°,
又∵AB=AC,
∴△ABC是等边三角形.
-
科目: 来源: 题型:
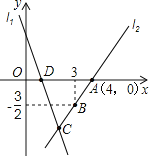
查看答案和解析>>【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.根据图中信息:
(1)求直线l2的解析表达式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,求出点P的坐标;
(4)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,∠ACB=90°,AC=BC=4,D为BC的中点,
中,∠ACB=90°,AC=BC=4,D为BC的中点, 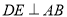 ,垂足为E.过点B作BF//AC交DE的延长线于点F,连接CF,AF.现有如下结论:
,垂足为E.过点B作BF//AC交DE的延长线于点F,连接CF,AF.现有如下结论:①BF=2;②
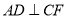 ;③AD平分∠CAB;④AF=
;③AD平分∠CAB;④AF=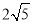 ;⑤∠CAF=∠CFB.其中正确的结论是( )
;⑤∠CAF=∠CFB.其中正确的结论是( )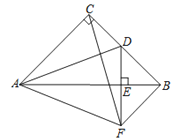
A. ①②③ B. ①②④ C. ②③④⑤ D. ①②④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:
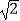 ≈1.41,
≈1.41,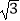 ≈1.73,
≈1.73, ≈2.45)
≈2.45)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程4(2﹣x)+x=ax的解为正整数,且关于x的不等式组
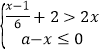 有解,则满足条件的所有整数a的值之和是( )
有解,则满足条件的所有整数a的值之和是( )A. 4 B. 0 C. ﹣1 D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D= , 求AE的长.
, 求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“筑梦少年正当时,不忘初心跟党走”知识竟赛中,七年级(2)班2人获一等奖,1人获二等奖,3人获三等奖,奖品价值41元;七年级(7)班1人获一等奖,3人获二等奖,3人获三等奖,奖品价值37元;七年级(13)班5人获二等奖,3人获三等奖,奖品价值_____元.
相关试题

