【题目】如图,线段 AB=24,动点 P 从 A 出发,以每秒 2 个单位的速度沿射线 AB运动,运动时间为 t 秒(t>0),M 为 AP 的中点.
(1)当点 P 在线段 AB 上运动时,
①当 t 为多少时,PB=2AM?②求2BM-BP的值.
(2)当 P 在 AB 延长线上运动时,N 为 BP 的中点,说明线段 MN 的长度不变,并 求出其值.
(3)在 P 点的运动过程中,是否存在这样的 t 的值,使 M、N、B 三点中的一个点 是以其余两点为端点的线段的中点,若有,请求出 t 的值;若没有,请说明理 由.
![]()
参考答案:
【答案】(1)①6②24(2)12(3)18或36
【解析】试题分析:(1)①分两种情况讨论:点P在点B左边;点P在点B右边,分别求出t的值即可;
②AM=x,BM=24﹣x,PB=24﹣2x,表示出2BM﹣BP后,化简即可得出结论;
(2)PA=2x,AM=PM=x,PB=2x﹣24,PN=![]() PB=x﹣12,表示出MN的长度,即可得到结论;
PB=x﹣12,表示出MN的长度,即可得到结论;
(3)分三种情况讨论:①当P在线段AB上时;②当P在线段AB的延长线上,M在线段AB上时;③当P和M都在线段AB的延长线上时.
试题解析:解:(1)①设出发x秒后PB=2AM,当点P在点B左边时,PA=2x,PB=24﹣2x,AM=x,由题意得:24﹣2x=2x,解得:x=6;
当点P在点B右边时,PA=2x,PB=2x﹣24,AM=x,由题意得:2x﹣24=2x,方程无解.
综上所述:出发6秒后PB=2AM.
②∵AM=x,BM=24﹣x,PB=24﹣2x,∴2BM﹣BP=2(24﹣x)﹣(24﹣2x)=24;
(2)∵PA=2x,AM=PM=x,PB=2x﹣24,PN=![]() PB=x﹣12,∴MN=PM﹣PN=x﹣(x﹣12)=12(定值);
PB=x﹣12,∴MN=PM﹣PN=x﹣(x﹣12)=12(定值);
(3)①当P在线段AB上时,如图1,有AP=2t,BP=24-2t,AM=MP=t,PN=NB=12-t,MN=12.若MN=NB,则12=12-t,解得t=0,不合题意,舍去.

②当P在线段AB的延长线上,M在线段AB上时,如图2,有AP=2t,BP=2t-24,AM=MP=t,MB=24-t, PN=NB=t-12.若MB=NB,则24-t=t-12,解得t=18.

③当P和M都在线段AB的延长线上时,如图3,有AP=2t,BP=2t-24,AM=MP=t,MB=t-24, PN=NB=t-12,MN=BN-BM=t-12-(t-24)=12.若MB=MN,则t-24= 12,解得t=36.
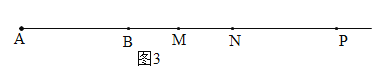
综上所述:t=18或36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为( )
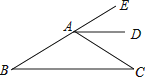
A.50°
B.40°
C.30°
D.20° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点 C 是线段 AB 上一点,且 5BC=2AB,D 是 AB 的中点,E 是CB 的中点,(1)若 DE=6,求 AB 的长;(2)求 AD:AC.
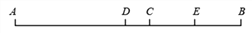
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4
B.2,3,2
C.3,2,0.4
D.3,3,2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于
 EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( ) 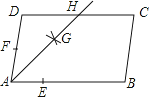
A.AG平分∠DAB
B.AD=DH
C.DH=BC
D.CH=DH -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )
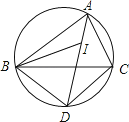
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI重合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在平行四边形ABCD中,AB=2,AD=4,∠ABC=60°,E为AD上一点,连接CE,AF∥CE且交BC于点F.
(1)求证:四边形AECF为平行四边形.
(2)证明:△AFB≌△CE D.
(3)DE等于多少时,四边形AECF为菱形.
(4)DE等于多少时,四边形AECF为矩形.

相关试题

