Question

【题目】如图，长方形OABC的边OC、OA分别在x轴、y轴上，点B的坐标为（，1）点D是AB边上一个动点（与点A不重合），沿OD将△OAD对折后，点A落到点P处，并满足△PCB是等腰三角形，则P点坐标为____.

Answer 1

【答案】（）或（ ）．

【解析】

连接PB，PC．分三种情况：①若PB=PC，设P（x，），过P作PH⊥x轴于H．在Rt△OPH中根据勾股定理解得x，从而确定P点坐标；②若BP=BC，则BP=1，连接OB．在Rt△OBC中根据勾股定理求出OB，从而得出P为线段OB中点，求出P点坐标；③若CP=CB，则CP=1，PO=PC，P在OC中垂线上．设P（，y），过P作PH⊥x轴于H，在Rt△OPH中根据勾股定理求出P点坐标即可．

连接PB，PC，

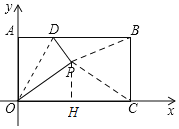
①若PB=PC，则P在BC的中垂线y=上，
∴设P（x，），
如图，过P作PH⊥x轴于H，
在Rt△OPH中，PH=，OH=x，OP=1，
∴x2+=1，
解得：x1=，x2=-（不合题意），
∴P（，）；
②若BP=BC，则BP=1，连接OB，
∵OP=1，
∴OP+PB=2，
∵在Rt△OBC中，∠OCB=90°，OB==2，
∴OP+PB=OB，
∴O，P，B三点共线，P为线段OB中点．
又∵B（，1），
∴P（，）；
③若CP=CB，则CP=1，
∵OP=1，
∴PO=PC，则P在OC的中垂线x=上，
∴设P（，y）．
过P作PH⊥x轴于H，在Rt△OPH中，PH=|y|，OH=，OP=1，
∴y2+=1，
解得：y1=，y2=-，
∴P（）或（），
当点P（）时，∠AOP=120°，此时∠AOD=60°，点D与点B重合，符合题意．
故答案为：（）或（ ）．