搜索
【题目】计算：|﹣4|﹣22+ 
﹣tan60°（说明：本题不允许使用计算器计算）
参考答案：
【答案】解：原式=4﹣4+2 
﹣ =
【解析】原式第一项利用绝对值的代数意义化简，第二项利用乘方的意义计算，第三项化为最简二次根式，最后一项利用特殊角的三角函数值计算即可得到结果．
【考点精析】本题主要考查了特殊角的三角函数值和实数的运算的相关知识点，需要掌握分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”；先算乘方、开方，再算乘除，最后算加减，如果有括号，先算括号里面的，若没有括号，在同一级运算中，要从左到右进行运算才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在ABCD中，SABCD=24，AE平分∠BAC，交BC于E，沿AE将△ABE折叠，点B的对应点为F，连接EF并延长交AD于G，EG将ABCD分为面积相等的两部分．则S△ABE= ．
-
科目： 来源： 题型：
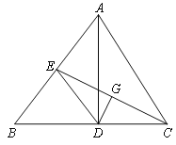
查看答案和解析>>【题目】如图，△ABC中，AD是高，CE是中线，点G是CE的中点，且DG⊥CE，垂足为点G．
(1)求证：DC=BE；
(2)若∠AEC=54°，求∠BCE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．
（1）求证：BE=CE；
（2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC是等边三角形，D是BC的中点．
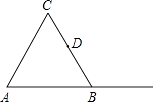
（1）作图： ①过B作AC的平行线BH；
②过D作BH的垂线，分别交AC，BH，AB的延长线于E，F，G．
（2）在图中找出一对全等的三角形，并证明你的结论． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD.
（1）求证：△ACE≌△ACF；
（2）若AB=21，AD=9，AC=17，求CF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【问题情境】
课外兴趣小组活动时，老师提出了如下问题：
如图①，△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE．请根据小明的方法思考：
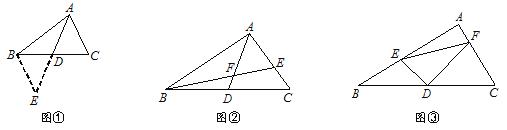
（1）由已知和作图能得到△ADC≌△EDB，依据是 ．
A．SSS B．SAS C．AAS D．HL
（2）由“三角形的三边关系”可求得AD的取值范围是 ．
解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
【初步运用】
如图②，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．若EF＝3，EC＝2，求线段BF的长．
【灵活运用】
如图③，在△ABC中， ∠A＝90°，D为BC中点， DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．试猜想线段BE、CF、EF三者之间的等量关系，并证明你的结论．
相关试题
