【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△ACE≌△ACF;
(2)若AB=21,AD=9,AC=17,求CF的长.

参考答案:
【答案】(1)证明见解析(2)8
【解析】
(1)由角平分线的定义及所给条件利用AAS可证明△ACE≌△ACF;
(2)结合(1)中的全等可证明Rt△CDF≌Rt△CEB,可得DF=BE,再由AE-AF,可证得DF=BE,利用线段和差可求得BE、AE,在Rt△BCE中可求得CE,则可求得CF.
(1)证明:∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴∠BAC=∠CAD, ∠AFC=∠AEC=90°
在△ACE和△ACF 中,
∵∠BAC=∠CAD, ∠AFC=∠AEC,AC=AC,
∴△ACE≌△ACF (AAS).
(2)由(1)知:∠AFC=∠AEC=90°,△ACE≌△ACF,
∴∠AFC=∠BEC=90°,CE=CF,AF=AE,
又∵CD=CB,
∴Rt△CDF≌Rt△CEB(HL),
∴DF=EB,
∴AD+DF=AF=AE=AB-EB,
∵AB=21,AD=9,
∴9+DF=21-EB,
∴EB=DF=6, AE=15,
在Rt△ACE中,![]()
∴CF=CE=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.

(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣4|﹣22+
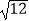 ﹣tan60°(说明:本题不允许使用计算器计算)
﹣tan60°(说明:本题不允许使用计算器计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D是BC的中点.
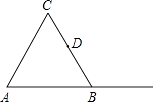
(1)作图: ①过B作AC的平行线BH;
②过D作BH的垂线,分别交AC,BH,AB的延长线于E,F,G.
(2)在图中找出一对全等的三角形,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
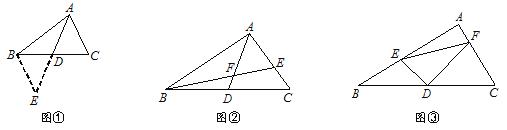
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两名射击运动员中选拔一名参加比赛,对这两名运动员进行测试,他们10次射击命中的环数如下:
甲
7
9
8
6
10
7
9
8
6
10
乙
7
8
9
8
8
6
8
9
7
10
根据测试成绩,你认为选择哪一名运动员参赛更好?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在对全市初中生的体质健康测试中,青少年体质研究中心随机抽取的10名女生的立定跳远的成绩(单位:厘米)如下:123,191,216,191,159,206,191,210,186,227.
(1)通过计算,样本数据(10名女生的成绩)的平均数是190厘米,中位数是多少厘米?众数是多少厘米?
(2)本市一初中女生的成绩是194厘米,你认为她的成绩如何?说明理由;
(3)研究中心分别确定了一个标准成绩,等于或大于这个成绩的女学生该项素质分别被评定为“合格”、“优秀”等级,其中合格的标准为大多数女生能达到,“优秀”的标准为全市有一半左右的学生能够达到,你认为标准成绩分别定为多少?说明理由;按拟定的合格标准,估计该市4650人中有多少人在合格以上?
相关试题

