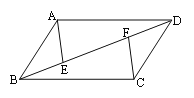
【题目】在ABCD中,SABCD=24,AE平分∠BAC,交BC于E,沿AE将△ABE折叠,点B的对应点为F,连接EF并延长交AD于G,EG将ABCD分为面积相等的两部分.则S△ABE= .
参考答案:
【答案】4
【解析】解:根据题意,AE平分∠BAC,交BC于E,沿AE将△ABE折叠,点B的对应点为F, ∴点F在对角线AC上,且S△ABE=S△AFE .
∵EG将ABCD分为面积相等的两部分,
∴点F为对角线AC的中点.
∴S△AFE=S△CFE(等底同高).
∵S平行四边形ABCD=24,
∴S△ABE=S△AFE=S△CFE= ![]() S△ABC=
S△ABC= ![]() S平行四边形ABCD=4.
S平行四边形ABCD=4.
故答案是:4.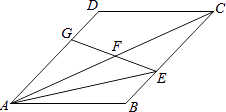
【考点精析】通过灵活运用平行四边形的性质和翻折变换(折叠问题),掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.
-
科目: 来源: 题型:
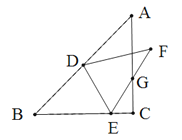
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=2,BC=AC,D为AB的中点,E为BC上一点,将△BDE沿DE翻折,得到△FDE,EF交AC于点G,则△ECG的周长是___________.
-
科目: 来源: 题型:
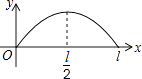
查看答案和解析>>【题目】点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )
A.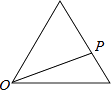
B.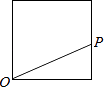
C.
D.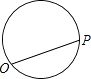
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:∣1-
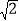 ∣+
∣+ 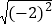 -(π-3.14)0
-(π-3.14)0(2)已知 (x-1)2 =16,求x的值
(3)已知8(x-1)3 -27=0,求x的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,AB∥CD,点E、F在线段BD上,且BE=DF,连接AE、CF.
(1)指出线段AE与CF的关系,并说明理由;
(2)若将题中的条件“点E、F在线段BD上”改为“点E、F在直线BD上” ,那么(1)中的结论还一定能成立吗?若能,直接写出结论;若不能,请举出反例加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,SABCD=24,AE平分∠BAC,交BC于E,沿AE将△ABE折叠,点B的对应点为F,连接EF并延长交AD于G,EG将ABCD分为面积相等的两部分.则S△ABE= .
-
科目: 来源: 题型:
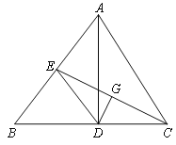
查看答案和解析>>【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,且DG⊥CE,垂足为点G.
(1)求证:DC=BE;
(2)若∠AEC=54°,求∠BCE的度数.
相关试题

