【题目】如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.

(1)求证:△ACE≌△BCF;
(2)若∠BFE=60°,求∠AEC的度数.
参考答案:
【答案】(1)见解析;(2)105°
【解析】
(1)根据同角的余角相等求出∠ACE=∠BCF,再利用“边角边”证明即可;
(2)根据等腰直角三角形的性质可得∠EFC=45°,然后求出∠BFC=105°,再根据全等三角形对应角相等解答.
证明:(1)∵△ABC和△EFC都是等腰直角三角形
∴CA=CB ,CE=CF
∵∠ACB=∠ECF=90°
∴∠ACE+∠ECB=∠ECB+∠BCF
∴∠ACE=∠BCF
∴△ACE≌△BCF(SAS)
(2)∵△EFC是等腰直角三角形
∴∠EFC=45°
∵∠BFE=60°
∴∠BFC=∠EFC +∠BFE=45°+ 60°= 105°
又∵△ACE≌△BCF
∴∠AEC=∠BFC=105°
-
科目: 来源: 题型:
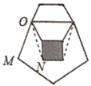
查看答案和解析>>【题目】如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,BC=1,
中,BC=1, .
.
(1)求AB的长度:
(2)过点A作AB的垂线,交AC的垂直平分线于点D ,以AB为一边作等边
 .
.①连接CE,求证: BD=CE;
②连接DE交AB于F.求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】用一条24cm的细绳围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=
 ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=
 ,AK=
,AK= ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=DE,AC=DF,BF=EC

(1)求证:△ABC≌△DEF;
(2)若
 ,求BF的长;
,求BF的长;(3)∠B=60°,∠D=70°,求∠AGD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 经过点A(
经过点A( ,0),B(
,0),B( ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

相关试题

