【题目】如图,在![]() 中,BC=1,
中,BC=1,![]() .
.

(1)求AB的长度:
(2)过点A作AB的垂线,交AC的垂直平分线于点D ,以AB为一边作等边![]() .
.
①连接CE,求证: BD=CE;
②连接DE交AB于F.求![]() 的值.
的值.
参考答案:
【答案】(1) AB=2; (2)①见解析;②![]()
【解析】
(1)由含30°角的直角三角形性质,得到AB=2BC=2即可;
(2)①连接CD,先证明△ACD是等边三角形,则DA=AC,由∠EAC=∠DAB=90°,AE=AB,即可得到![]() ,然后得到BD=CE;
,然后得到BD=CE;
②作EH⊥AB于H ,由![]() ,
,![]() 得到
得到![]() ,则得到
,则得到![]() ,可证
,可证![]() ,然后得到EF=DF,即可得到答案.
,然后得到EF=DF,即可得到答案.
(1)解:∵在![]() 中,∠BAC=30°,
中,∠BAC=30°,
∴AB=2BC=2;
(2)①证明:连接 CD,
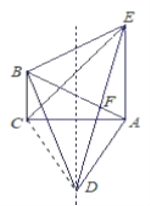
![]() 为等边三角形,
为等边三角形,
∴AB=AE,∠EAB = 60°,
∵∠BAC=30°,AB⊥AD,
∴∠DAC=60°,
∴∠EAC=∠DAB,
又∵ DC=DA,
∴△ADC为等边三角形,
![]() .
.
在![]() 与
与![]() 中,
中,
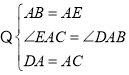
![]() ,
,
∴BD=CE;
②解:作EH⊥AB于H .
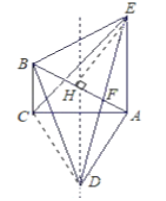
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
![]()
![]() ,
,
![]() .
.
又![]() ,
,
在![]() 与
与![]() 中,
中,
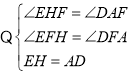 ,
,
![]() , .
, .
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点的坐标为A(3,4),B(1,2), C(5, 1).
(1)写出A、B、C关于y轴对称的点A1、B1、C1的坐标: A1_____、 B1 、C1 ;
(2)若
 各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A'、B'、C',并依次连接这三个点,判断所得△A′B′C′与原
各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A'、B'、C',并依次连接这三个点,判断所得△A′B′C′与原 有怎样的位置关系。
有怎样的位置关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1﹣5m)x﹣5与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.
-
科目: 来源: 题型:
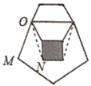
查看答案和解析>>【题目】如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条24cm的细绳围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.

(1)求证:△ACE≌△BCF;
(2)若∠BFE=60°,求∠AEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=
 ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=
 ,AK=
,AK= ,求CN的长.
,求CN的长.
相关试题

