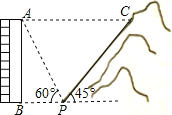
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内。
(1)求居民楼AB的高度;
(2)求C、A之间的距离。(精确到0.1m,参考数据: ![]() )
)
参考答案:
【答案】(1)居民楼AB的高度为21.2m;
(2)C、A之间的距离为33.4m。
【解析】(1)首先分析图形:根据题意构造直角三角形,利用在Rt△CPE中,由sin45°=CEPC ,得出EC的长度,进而可求出答案.(2)在Rt△CPE中,tan60°=AB BP
,得出BP的长,进而得出PE的长,即可得出答案.
解:(1)过点C作CE⊥BP于点E,
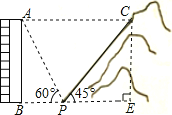
在Rt△CPE中
∵PC=30m,∠CPE=45°,
∴sin45°=![]() ,
,
∴CE=PCsin45°=30×![]() =15m,
=15m,
∵点C与点A在同一水平线上,
∴AB=CE=15![]() ≈21.2m,
≈21.2m,
答:居民楼AB的高度约为21.2m;
(2)在Rt△ABP中,∵∠APB=60°,
∴tan60°=![]() ,
,
∴BP=![]() m,
m,
∵PE=CE=15 m,
∴AC=BE=15![]() +5
+5![]() ≈33.4m,
≈33.4m,
答:C、A之间的距离约为33.4m.
“点睛”此题主要考查了仰角、坡角问题的应用,要求学生借助仰角、坡角关系构造直角三角形,并结合图形利用三角函数求解.
-
科目: 来源: 题型:
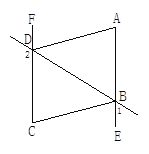
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出了如下表格:
x
…
-1
0
1
2
3
4
…
y=ax2+bx+c(a≠0)
…
8
3
0
-1
0
3
…
那么当该二次函数值y > 0时,x的取值范围是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB//CD,求证:
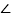 B+
B+ D+
D+ BED=360°(至少用三种方法)
BED=360°(至少用三种方法)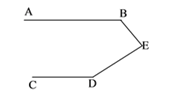
-
科目: 来源: 题型:
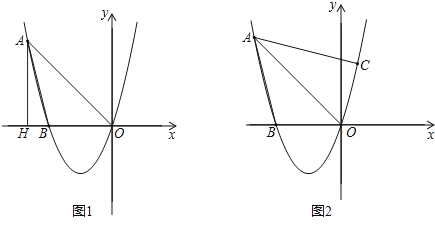
查看答案和解析>>【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:5x+2=3(x+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2x2)3+2x2x4
相关试题

