【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
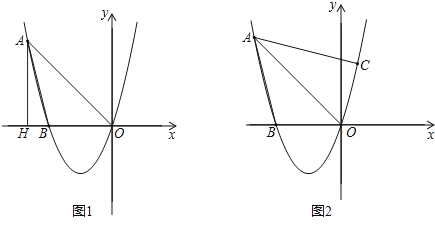
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;
;
(2)∠AOP=∠AOH+∠POH=45o+45o=90o;
(3)存在,直线AC解析式为![]()
【解析】试题分析:(1)根据已知点的坐标利用待定系数法确定二次函数的解析式即可;
(2)设点P坐标为(m,m2+3m),从而得到直线OA的解析式为y=-x,然后表示出点Q的坐标为(m,-m),进而表示出PQ=-m-(m2+3m)=-m2-4m,利用当四边形AHPQ为平行四边形时,PQ=AH=4得到-m2-4m=4,从而求得m的值,进而确定答案;
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,从而证得△AOD≌△AOB后表示点D坐标为(0,3),从而确定直线AC解析式,
试题解析:(1)由题意,得
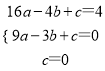 ,解得
,解得![]() .
.
∴抛物线的解析式为y=x2+3x;
(2)设点P坐标为(m,m2+3m),其中-4<m<0
∵点A(-4,4),
∴直线OA的解析式为y=-x,
从而点Q的坐标为(m,-m)
∴PQ=-m-(m2+3m)=-m2-4m,
当四边形AHPQ为平行四边形时,PQ=AH=4,
即-m2-4m=4,解得m=-2
此时点P坐标为(-2,-2)
∴∠AOP=∠AOH+∠POH=45°+45°=90°.
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,
∵∠CAO=∠BAO,AO=AO,
∴△AOD≌△AOB,
∴OD=OB=3,点D坐标为(0,3),
设直线AC解析式为y=px+q,则![]()
解得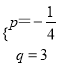 ,
,
∴直线AC解析式为y=![]() x+3
x+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出了如下表格:
x
…
-1
0
1
2
3
4
…
y=ax2+bx+c(a≠0)
…
8
3
0
-1
0
3
…
那么当该二次函数值y > 0时,x的取值范围是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB//CD,求证:
 B+
B+ D+
D+ BED=360°(至少用三种方法)
BED=360°(至少用三种方法)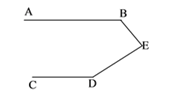
-
科目: 来源: 题型:
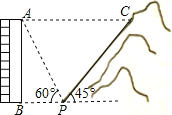
查看答案和解析>>【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内。
(1)求居民楼AB的高度;
(2)求C、A之间的距离。(精确到0.1m,参考数据:
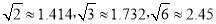 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:5x+2=3(x+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2x2)3+2x2x4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是 ( )
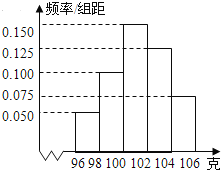
A. 90 B. 75 C. 60 D. 45
相关试题

