【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.
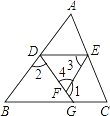
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=________.(________.),
∴AB∥EF(________.)
∴∠3=________.(________.)
又∠B=∠3(已知)
∴∠B=________.(等量代换)
∴DE∥BC(________.)
∴∠C=∠AED(________.).
参考答案:
【答案】 ∠DFE; 同角的补角相等; 内错角相等,两直线平行; ∠ADE; 两直线平行,内错角相等; ∠ADE; 同位角相等,两直线平行; 两直线平行,同位角相等
【解析】根据平行线的判定及性质即可证明.
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=∠DFE.(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行)
∴∠3=∠ADE.(两直线平行,内错角相等)
又∠B=∠3(已知)
∴∠B=∠ADE.(等量代换)
∴DE∥BC(同位角相等,两直线平行)
∴∠C=∠AED(两直线平行,同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣4x﹣4的顶点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+x+c与x轴交点的横坐标为﹣1,则a+c= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:
①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE .
其中正确结论有( )个.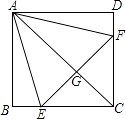
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请在横线上填写合适的内容,完成下面的证明:
如图1,AB∥CD,求证:∠B+∠D=∠BED.
证明:过点E引一条直线EF∥AB
∴∠B=∠BEF,(___________)
∵AB∥CD,EF∥AB
∴EF∥CD(___________)
∴∠D=________(___________)
∴∠B+∠D=∠BEF+∠FED
即∠B+∠D=∠BED.
(2)如图2,AB∥CD,请写出∠B+∠BED+∠D=360°的推理过程.________
(3)如图3,AB∥CD,请直接写出结果∠B+∠BEF+∠EFD+∠D=________

-
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b是方程x2+x﹣2021=0的两个实数根,则(a﹣1)(b﹣1)的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2(________)
∵AC∥DE(已知)
∴∠1=∠3(________)
故∠2=∠3(________)
∵DF∥AE(已知)
∴∠2=∠5(________)
∴∠3=∠4(________)
∴DE平分∠BDE(________)

相关试题

