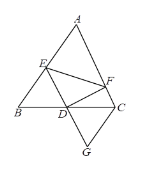
【题目】如图,在△ABC中,D为BC的中点,E为AB上一点,DF⊥DE交AC于点F,延长ED至点G,使GD=ED,连接CG.
(1)求证:BE=CG;
(2)求证:BE+CF>EF.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)由点D为BC的中点,ED=GD,利用SAS,即可判定△BDE≌△CDG,又由全等三角对应边相等,证得BE=CG.
(2)首先连接FG,由线段垂直平分线的性质,可证得EF=FG,结合BE=CG,由三角形三边关系,即可证得结论.
解: (1) 在△BDE和△CDG中,
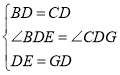 ,
,
∴△BDE≌△CDG (SAS),
∴BE=CG;
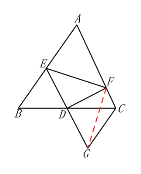
(2) 连接FG
∵ED=GD,DF⊥DE,
∴EF=GF,
在△CFG中, CF+CG>GF,
∵BE=CG,
∴BE+CF>EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A、B两个顶点在
 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A.
 B.
B.  C.
C.  D.
D. 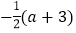
-
科目: 来源: 题型:
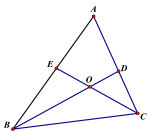
查看答案和解析>>【题目】如图,已知,△ABC中,∠A=60,BD,CE是△ABC的两条角平分线,BD,CE相交于点O,求证:BC=CD+BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC的垂直平分线MN分别交AB,AC于D,E.若AE=5,△BCD的周长17,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请参照下面探究过程,完成所提出的问题.
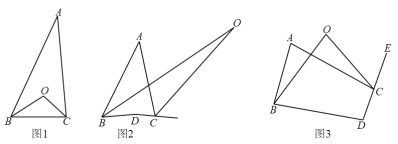
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点.
若∠A=30°,则∠BOC= ;
若∠A=α,则∠BOC= (用含α的代数式表示)
(2)如图2,在四边形ABDC中,点O是∠ABD和∠ACD外角平分线的交点,写出∠A、∠D与∠O之间的数量关系,并说明理由;
(3) 如图3,在四边形ABDC中,∠ABD和∠ACD外角的n等分线交于O,使∠ABD=n∠ABO,∠ACE=n∠ACO.直接写出∠A、∠D和∠O之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
相关试题

