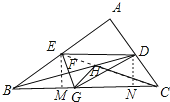
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2 ![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
参考答案:
【答案】
(1)
解:四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
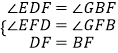 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形
(2)
解:作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,
在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2 ![]() ,
,
∴EM= ![]() BE=
BE= ![]() ,
,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN= ![]() ,MN=DE=2
,MN=DE=2 ![]() ,
,
在RT△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC= ![]() ,
,
∴MC=3 ![]() ,
,
在RT△EMC中,∵∠EMC=90°,EM= ![]() .MC=3
.MC=3 ![]() ,
,
∴EC= ![]() =
= ![]() =10
=10 ![]() .
.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为10 ![]()
【解析】(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识,解题的关键是利用对称找到点H的位置,属于中考常考题型.
【考点精析】根据题目的已知条件,利用角平分线的性质定理和平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)求证:四边形DEBF是平行四边形;
(3)若OD=OE=OF,则四边形DEBF是什么特殊的四边形,请证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.

(1)求证:PF平分∠BFD.
(2)若tan∠FBC= ,DF=
,DF=  ,求EF的长.
,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为x(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2﹣
x2﹣  x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C 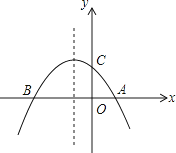
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.

(1)求DC的长;
(2)求AB的长;
(3)求证:△ABC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入
 表是某周的生产情况
表是某周的生产情况 超产为正、减产为负
超产为正、减产为负 :
: 星期
一
二
三
四
五
六
日
增减
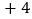
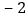
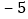

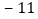
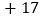
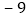
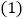 根据记录可知前三天共生产多少辆;
根据记录可知前三天共生产多少辆; 产量最多的一天比产量最少的一天多生产多少辆;
产量最多的一天比产量最少的一天多生产多少辆; 该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
相关试题

