【题目】星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为x(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家。
参考答案:
【答案】
(1)
解:由题意,得y1=20x (0≤x≤2)
y2=40(x﹣1)(1≤x≤2);
(2)
解:由题意得;

(3)
由图象得同时到达老家
【解析】(1)根据速度乘以时间等于路程,可得函数关系式,(2)根据描点法,可得函数图象;(3)根据图象,可得答案.本题考查了一次函数图象,利用描点法是画函数图象的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运动员在一场篮球比赛中的技术统计如表所示:
技术
上场时间(分钟)
出手投篮(次)
投中
(次)罚球得分
篮板
(个)助攻(次)
个人总得分
数据
46
66
22
10
11
8
60
注:表中出手投篮次数和投中次数均不包括罚球.
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)求证:四边形DEBF是平行四边形;
(3)若OD=OE=OF,则四边形DEBF是什么特殊的四边形,请证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.

(1)求证:PF平分∠BFD.
(2)若tan∠FBC= ,DF=
,DF=  ,求EF的长.
,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.

(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2﹣
x2﹣  x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C 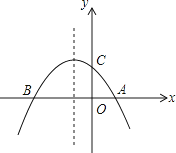
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.

(1)求DC的长;
(2)求AB的长;
(3)求证:△ABC是直角三角形.
相关试题

