【题目】如图,平面直角坐标系中,![]() 的顶点坐标为:
的顶点坐标为:![]() ,
,![]() ,
,![]() .
.

(1)将![]() 向左平移2个单位长度,再向上平移1个单位长度,得
向左平移2个单位长度,再向上平移1个单位长度,得![]() .画出
.画出![]() 并写出
并写出![]() 的顶点坐标;
的顶点坐标;
(2)请判断![]() 的形状并求它的面积.
的形状并求它的面积.
参考答案:
【答案】(1)图形见解析;A′(-1,3),B′(0,0),C′(2,4);(2)等腰直角三角形;△ABC的面积为5
【解析】
(1)根据平移的定义分别作出三个顶点平移后的对应点,再顺次连接即可得;
(2)利用勾股定理及其逆定理,即可得到△ABC的形状,进而得出其面积.
(1)如图所示,△A'B'C'即为所求,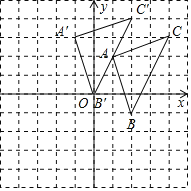
∴点A′(-1,3),B′(0,0),C′(2,4);
(2)由勾股定理可得,AB=![]() ,AC=
,AC=![]() ,BC=2
,BC=2![]() ,
,
∴AB2+AC2=BC2,AB=AC,
∴△ABC是等腰直角三角形,
∴△ABC的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=
 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2与y轴交于点C(0,4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.
(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连结CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,
是等边三角形, 是
是 边上的一点,连接
边上的一点,连接 ,把
,把 绕着点
绕着点 逆时针旋转
逆时针旋转 ,得到
,得到 ,连接
,连接 ,若
,若 ,
, ,则
,则 的周长是( )
的周长是( )
A.16B.15C.13D.12
-
科目: 来源: 题型:
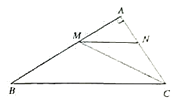
查看答案和解析>>【题目】如图,在
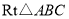 中,
中,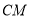 平分
平分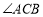 交
交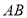 边于点
边于点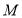 ,过点
,过点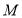 作
作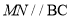 交
交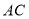 边于点
边于点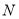 .且
.且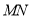 平分
平分 ,若
,若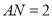 .
.
(1)求
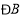 的度数.
的度数.(2)求
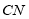 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的
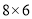 的方格中,
的方格中,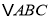 和
和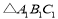 的顶点都在格点上,且
的顶点都在格点上,且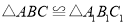 .利用平移、旋转变换,能使
.利用平移、旋转变换,能使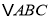 通过一次或两次变换后与
通过一次或两次变换后与 完全重合.
完全重合.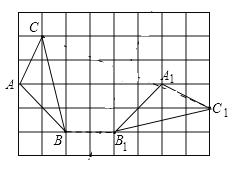
(1)请你写出
 通过两次变换与
通过两次变换与 完全重合的变换过程.
完全重合的变换过程.(2)
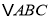 通过一次旋转就能得到
通过一次旋转就能得到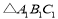 .请在图中标出旋转中心
.请在图中标出旋转中心 ,并简要说明你是如何确定的.
,并简要说明你是如何确定的. -
科目: 来源: 题型:
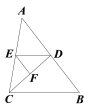
查看答案和解析>>【题目】如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.
(1)试判断∠DEF与∠B的大小关系,并说明理由;
(2)若D、E、F分别是AB、AC、CD边上的中点,S△DEF=4,求S△ABC.
相关试题

