【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是
是![]() 边上的一点,连接
边上的一点,连接![]() ,把
,把![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的周长是( )
的周长是( )

A.16B.15C.13D.12
参考答案:
【答案】D
【解析】
根据旋转的性质得到△BDE是等边三角形得到DE=BD=5,由旋转的性质得到AE=CD,所以△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD.
∵△ABC是等边三角形,BC=7,
∴AC=BC=7,
∵将△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,
∴DE=BD=5,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+5=5+7=12.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,
(1)如图1,若AB∥ON,则
①∠ABO的度数是______;
②当∠BAD=∠ABD时,x=______;
当∠BAD=∠BDA时,x=______;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=
 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2与y轴交于点C(0,4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.
(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连结CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
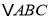 的顶点坐标为:
的顶点坐标为: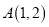 ,
,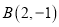 ,
,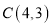 .
.
(1)将
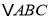 向左平移2个单位长度,再向上平移1个单位长度,得
向左平移2个单位长度,再向上平移1个单位长度,得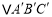 .画出
.画出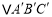 并写出
并写出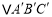 的顶点坐标;
的顶点坐标;(2)请判断
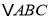 的形状并求它的面积.
的形状并求它的面积. -
科目: 来源: 题型:
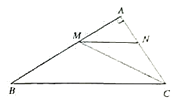
查看答案和解析>>【题目】如图,在
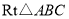 中,
中,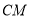 平分
平分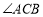 交
交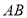 边于点
边于点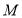 ,过点
,过点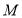 作
作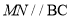 交
交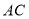 边于点
边于点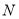 .且
.且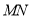 平分
平分 ,若
,若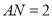 .
.
(1)求
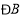 的度数.
的度数.(2)求
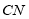 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的
 的方格中,
的方格中,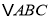 和
和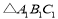 的顶点都在格点上,且
的顶点都在格点上,且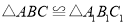 .利用平移、旋转变换,能使
.利用平移、旋转变换,能使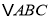 通过一次或两次变换后与
通过一次或两次变换后与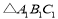 完全重合.
完全重合.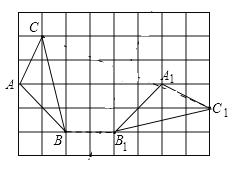
(1)请你写出
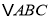 通过两次变换与
通过两次变换与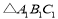 完全重合的变换过程.
完全重合的变换过程.(2)
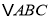 通过一次旋转就能得到
通过一次旋转就能得到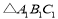 .请在图中标出旋转中心
.请在图中标出旋转中心 ,并简要说明你是如何确定的.
,并简要说明你是如何确定的.
相关试题

