【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 边于点
边于点![]() .且
.且![]() 平分
平分![]() ,若
,若![]() .
.
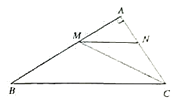
(1)求![]() 的度数.
的度数.
(2)求![]() 的长.
的长.
参考答案:
【答案】(1)30°;(2)4
【解析】
(1)根据角平分线的定义及平行线的性质可求得∠B=∠BCM=∠ACM,再根据∠ A=90°,即可求得∠B的度数;
(2)由(1)可求得∠AMN=∠B=30°,∠MCN=∠CMN ,进而可求得MN=2AN=4,MN=CN,即可解答.
(1)∵CM平分∠ACB,MN平分∠AMC,
∴∠ACM=∠BCM,∠AMN=∠CMN,
又∵MN∥BC,
∴∠AMN=∠B,∠CMN=∠BCM,
∴∠B=∠BCM=∠ACM,
∵∠A=90°,
∴∠B=![]() ×90°=30°;
×90°=30°;
(2)由(1)得,∠AMN=∠B=30°,∠MCN=∠CMN,∠A=90°,
∴MN=2AN=4,MN=CN,
∴CN=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2与y轴交于点C(0,4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.
(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连结CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,
是等边三角形, 是
是 边上的一点,连接
边上的一点,连接 ,把
,把 绕着点
绕着点 逆时针旋转
逆时针旋转 ,得到
,得到 ,连接
,连接 ,若
,若 ,
, ,则
,则 的周长是( )
的周长是( )
A.16B.15C.13D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
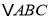 的顶点坐标为:
的顶点坐标为: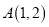 ,
,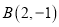 ,
,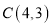 .
.
(1)将
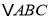 向左平移2个单位长度,再向上平移1个单位长度,得
向左平移2个单位长度,再向上平移1个单位长度,得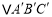 .画出
.画出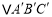 并写出
并写出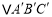 的顶点坐标;
的顶点坐标;(2)请判断
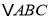 的形状并求它的面积.
的形状并求它的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的
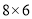 的方格中,
的方格中,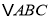 和
和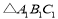 的顶点都在格点上,且
的顶点都在格点上,且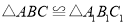 .利用平移、旋转变换,能使
.利用平移、旋转变换,能使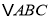 通过一次或两次变换后与
通过一次或两次变换后与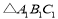 完全重合.
完全重合.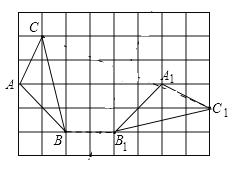
(1)请你写出
 通过两次变换与
通过两次变换与 完全重合的变换过程.
完全重合的变换过程.(2)
 通过一次旋转就能得到
通过一次旋转就能得到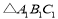 .请在图中标出旋转中心
.请在图中标出旋转中心 ,并简要说明你是如何确定的.
,并简要说明你是如何确定的. -
科目: 来源: 题型:
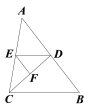
查看答案和解析>>【题目】如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.
(1)试判断∠DEF与∠B的大小关系,并说明理由;
(2)若D、E、F分别是AB、AC、CD边上的中点,S△DEF=4,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧
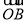 上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.
上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.(1)求证:PD2=PEPF;
(2)当∠BOP=30°,P点为OB的中点时,求D、E、F、P四个点的坐标及S△DEF.
相关试题

