【题目】下列命题:
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
![]() 若
若![]() ,则一元二次方程
,则一元二次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
![]() 若
若![]() ,则二次函数
,则二次函数![]() 的图象与坐标轴的公共点的个数是2或3.
的图象与坐标轴的公共点的个数是2或3.
其中正确的是![]()
A. 只有![]() B. 只有
B. 只有![]() C. 只有
C. 只有![]() D. 只有
D. 只有![]()
参考答案:
【答案】B
【解析】试题解析:①b2-4ac=(-a-c)2-4ac=(a-c)2≥0,正确;
②若b>a+c,则△的大小无法判断,故不能得出方程有两个不等实根,错误;
③b2-4ac=4a2+9c2+12ac-4ac=4(a+c)2+5c2,因为a≠0,故(a+c)2与c2不会同时为0,所以b2-4ac>0,正确;
④二次函数y=ax2+bx+c与y轴必有一个交点,而这个交点有可能跟图象与x轴的交点重合,故正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是半径为3的⊙O上的点,
 尺规作图:作⊙O的内接正六边形ABCDEF;
尺规作图:作⊙O的内接正六边形ABCDEF; 求
求 中弧AC的长.
中弧AC的长.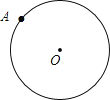
-
科目: 来源: 题型:
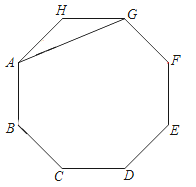
查看答案和解析>>【题目】如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕
 )的值;
)的值;(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上从左到右的三个点
 ,
, ,
, 所对应的数分别为
所对应的数分别为 ,
, ,
, .其中
.其中 ,
, ,如图所示.
,如图所示.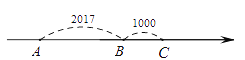
(1)若以
 为原点,写出点
为原点,写出点 ,
, 所对应的数,并计算
所对应的数,并计算 的值.
的值. (2)若原点
 在
在 ,
, 两点之间,求
两点之间,求 的值.
的值. (3)若
 是原点,且
是原点,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1)、B(0,﹣2)、C(1,0),点P(0,2)绕点A旋转180°得到点
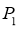 ,点
,点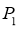 绕点B旋转180°得到点
绕点B旋转180°得到点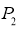 ,点
,点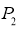 绕点C旋转180°得到点
绕点C旋转180°得到点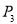 ,点
,点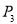 绕点A旋转180°得到点
绕点A旋转180°得到点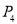 ,…,按此作法进行下去,则点
,…,按此作法进行下去,则点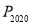 的坐标为( )
的坐标为( )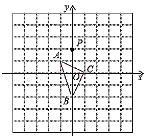
A.(0,4)B.(﹣2,0)C.(2,﹣4)D.(﹣2,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
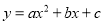 的图象上部分点的横坐标x与纵坐标y的对应值如下表:
的图象上部分点的横坐标x与纵坐标y的对应值如下表:x

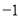
0
1
2

y

0
3
4
3

那么关于它的图象,下列判断正确的是
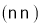
A. 开口向上 B. 与x轴的另一个交点是
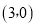
C. 与y轴交于负半轴 D. 在直线
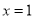 的左侧部分是下降的
的左侧部分是下降的
相关试题

