【题目】综合与实践
操作发现
如图,在平面直角坐标系中,已知线段![]() 两端点的坐标分别为
两端点的坐标分别为![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 沿
沿![]() 方向平移,平移的距离为
方向平移,平移的距离为![]() 的长度.
的长度.

(1)画出![]() 平移后的线段
平移后的线段![]() ,直接写出点
,直接写出点![]() 对应点
对应点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() ,
,![]() ,已知
,已知![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
拓展探索
(3)若点![]() 为线段
为线段![]() 上一动点(不含端点),连接
上一动点(不含端点),连接![]() ,
,![]() ,试猜想
,试猜想![]() ,
,![]() 和
和![]() 之间的关系,并说明理由.
之间的关系,并说明理由.
参考答案:
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)按要求作出图形,并根据平移的性质写出点N的坐标即可;
(2)由平移的性质可得出![]() ,
,![]() ,再由平行的性质和角平分线的定义可得出
,再由平行的性质和角平分线的定义可得出![]() ;
;
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,由平行的性质容易证明
,由平行的性质容易证明![]() 。
。
解:(1)所作线段![]() 如图所示.
如图所示.

点![]() 的坐标为
的坐标为![]() .
.
(2)证明:根据平移的性质,可知,![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
(3)![]() .
.
理由如下:
如图,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
又∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N.连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图①,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(
 ,0),B(3,0),与y轴交于点C,连接BC.
,0),B(3,0),与y轴交于点C,连接BC.(1)求抛物线的表达式;
(2)抛物线上是否存在点M,使得△MBC的面积与△OBC的面积相等,若存在,请直接写出点M的坐标;若不存在,请说明理由;
(3)点D(2,m)在第一象限的抛物线上,连接BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC,BE,则下列结论:①AC=AD;②AO=
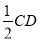 ;③四边形ACBE是菱形;④
;③四边形ACBE是菱形;④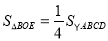 .其中正确的结论有____.(填写所有正确结论的序号)
.其中正确的结论有____.(填写所有正确结论的序号)
相关试题

