搜索
【题目】小李是某服装厂的一名工人，负责加工A，B两种型号服装，他每月的工作时间为22天，月收入由底薪和计件工资两部分组成，其中底薪900元，加工A型服装1件可得20元，加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件，设他每月加工A型服装的时间为x天，月收入为y元.
(1) 求y与x的函数关系式；
(2) 根据服装厂要求，小李每月加工A型服装数量应不少于B型服装数量的
，那么他的月收入最高能达到多少元？
参考答案：
【答案】(1)
;(2)2820元.
【解析】
试题分析：（1）根据月收入=A型服装的收入+B型服装的收入+D底薪，代入数值即可得y与x的函数关系式；（2）根据小李每月加工A型服装数量应不少于B型服装数量的
，列出不等式，求出x的取值范围，再根据一次函数的性质可求得小李的最高月收入.
试题解析：(1) 
即.
(2) 依题意，得
∴
.
在中，
，
∴
随
的增大而减小.
∴当=12时，取最大值，此时
.
答：当小李每月加工A型服装12天时，月收入最高，可达2820元.
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：有三个内角相等的四边形叫三等角四边形．
（1）三等角四边形ABCD中，∠A=∠B=∠C，求∠A的取值范围；
（2）如图，折叠平行四边形纸片DEBF，使顶点E，F分别落在边BE，BF上的点A，C处，折痕分别为DG，DH．求证：四边形ABCD是三等角四边形．
-
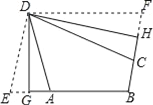
科目： 来源： 题型：
查看答案和解析>>【题目】满足下列条件的三角形中，是直角三角形的是（ ）
A.三角形的三边长满足关系a+b＝c
B.三角形的三边长之比2：3：4
C.三角形的三边长分别为5、12、13
D.三角形的一边长等于另一边长的一半
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程3x﹣2a=7的解是2，则a的值为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y＝x2﹣6x+5向上平移3个单位长度，再向左平移2个单位长度后，得到的抛物线解析式是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点，抛物线
过A、B两点，且与x轴交于另一点C．（1）求b、c的值；
（2）如图1，点D为AC的中点，点E在线段BD上，且BE=2ED，连接CE并延长交抛物线于点M，求点M的坐标；
（3）将直线AB绕点A按逆时针方向旋转15°后交y轴于点G，连接CG，如图2，P为△ACG内以点，连接PA、PC、PG，分别以AP、AG为边，在他们的左侧作等边△APR，等边△AGQ，连接QR
①求证：PG=RQ；
②求PA+PC+PG的最小值，并求出当PA+PC+PG取得最小值时点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB∥DC，E是AD中点，EF⊥BC于点F，BC=5，EF=3．
（1）若AB=DC，则四边形ABCD的面积S=__；
（2）若AB＞DC，则此时四边形ABCD的面积S′__S（用“＞”或“=”或“＜”填空）．
相关试题
