【题目】如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线![]() 过A、B两点,且与x轴交于另一点C.
过A、B两点,且与x轴交于另一点C.
(1)求b、c的值;
(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内以点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.

参考答案:
【答案】(1)b=﹣2,c=3;(2)M(![]() ,
,![]() );(3)①证明见解析;②PA+PC+PG的最小值为
);(3)①证明见解析;②PA+PC+PG的最小值为![]() ,此时点P的坐标(﹣
,此时点P的坐标(﹣![]() ,
,![]() ).
).
【解析】
试题分析:(1)把A(﹣3,0),B(0,3)代入抛物线![]() 即可解决问题.
即可解决问题.
(2)首先求出A、C、D坐标,根据BE=2ED,求出点E坐标,求出直线CE,利用方程组求交点坐标M.
(3)①欲证明PG=QR,只要证明△QAR≌△GAP即可.②当Q、R、P、C共线时,PA+PG+PC最小,作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K,由sin∠ACM=![]() =
=![]() 求出AM,CM,利用等边三角形性质求出AP、PM、PC,由此即可解决问题.
求出AM,CM,利用等边三角形性质求出AP、PM、PC,由此即可解决问题.
试题解析:(1)∵一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,∴A(﹣3,0),B(0,3),∵抛物线![]() 过A、B两点,∴
过A、B两点,∴![]() ,解得:
,解得:![]() ,∴b=﹣2,c=3.
,∴b=﹣2,c=3.
(2),对于抛物线![]() ,令y=0,则
,令y=0,则![]() ,解得x=﹣3或1,∴点C坐标(1,0),∵AD=DC=2,∴点D坐标(﹣1,0),∵BE=2ED,∴点E坐标(
,解得x=﹣3或1,∴点C坐标(1,0),∵AD=DC=2,∴点D坐标(﹣1,0),∵BE=2ED,∴点E坐标(![]() ,1),设直线CE为y=kx+b,把E、C代入得到:
,1),设直线CE为y=kx+b,把E、C代入得到: ,解得:
,解得: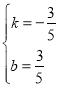 ,∴直线CE为
,∴直线CE为![]() ,由
,由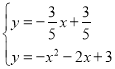 ,解得
,解得![]() 或
或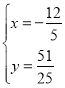 ,∴点M坐标(
,∴点M坐标(![]() ,
,![]() ).
).
(3)①∵△AGQ,△APR是等边三角形,∴AP=AR,AQ=AG,∠QAC=∠RAP=60°,∴∠QAR=∠GAP,在△QAR和△GAP中,∵AQ=AG,∠QAR=∠GAP,AR=AP,∴△QAR≌△GAP,∴QR=PG.
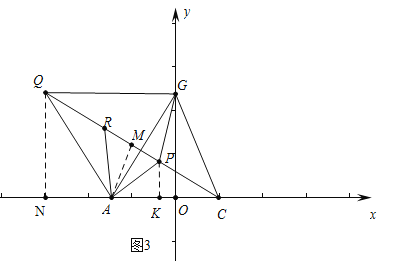
②如图3中,∵PA+PB+PC=QR+PR+PC=QC,∴当Q、R、P、C共线时,PA+PG+PC最小,作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K.∵∠GAO=60°,AO=3,∴AG=QG=AQ=6,∠AGO=30°,∵∠QGA=60°,∴∠QGO=90°,∴点Q坐标(﹣6,![]() ),在RT△QCN中,QN=
),在RT△QCN中,QN=![]() ,CN=7,∠QNC=90°,∴QC=
,CN=7,∠QNC=90°,∴QC=![]() =
=![]() ,∵sin∠ACM=
,∵sin∠ACM=![]() =
=![]() ,∴AM=
,∴AM=![]() ,∵△APR是等边三角形,∴∠APM=60°,∵PM=PR,cos30°=
,∵△APR是等边三角形,∴∠APM=60°,∵PM=PR,cos30°=![]() ,∴AP=
,∴AP=![]() ,PM=RM=
,PM=RM=![]() ,∴MC=
,∴MC=![]() =
=![]() ,∴PC=CM﹣PM=
,∴PC=CM﹣PM=![]() ,∵
,∵![]() ,∴CK=
,∴CK=![]() ,PK=
,PK=![]() ,∴OK=CK﹣CO=
,∴OK=CK﹣CO=![]() ,∴点P坐标(﹣
,∴点P坐标(﹣![]() ,
,![]() ),∴PA+PC+PG的最小值为
),∴PA+PC+PG的最小值为![]() ,此时点P的坐标(﹣
,此时点P的坐标(﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程3x﹣2a=7的解是2,则a的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1) 求y与x的函数关系式;
(2) 根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的
 ,那么他的月收入最高能达到多少元?
,那么他的月收入最高能达到多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣6x+5向上平移3个单位长度,再向左平移2个单位长度后,得到的抛物线解析式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+3x=1,则多项式3x2+9x﹣1的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)8+(―
 )―5―(―0.25) (2)―82+72÷36
)―5―(―0.25) (2)―82+72÷36(3)7 ×1 ÷(-9+19) (4)25×(―18)+(―25)×12+25×(-10 )
(5)(-79)÷2 +
 ×(-29) (6)(-1)3-(1-7)÷3×[3―(―3)2]
×(-29) (6)(-1)3-(1-7)÷3×[3―(―3)2](7)2(x-3)-3(-x+1) (8) –a+2(a-1)-(3a+5)
相关试题

