【题目】已知a是最大的负整数,b是多项式2m2n﹣m3n2﹣m﹣2的次数,c是单项式﹣2xy2的系数,且a、b、c分别是点A、B、C在数轴上对应的数.
![]()
(1)求a、b、c的值,并在数轴上标出点A、B、C.
(2)若M点在此在此数轴上运动,请求出M点到AB两点距离之和的最小值;
(3)若动点P、Q同时从A、B出发沿数轴负方向运动,点P的速度是每秒![]() 个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q能追上点P?
个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q能追上点P?
(4)在数轴上找一点N,使点M到A、B、C三点的距离之和等于10,请直接写出所有的N对应的数.(不必说明理由)
参考答案:
【答案】(1)a=﹣1,b=5,c=﹣2,数轴详见解析;(2)6;(3)运动4秒后,点Q可以追上点P;(4)M对应的数为2或﹣2![]() .
.
【解析】
(1)根据题意易得a,b,c的值,然后在数轴上表示出来即可;
(2)当M点在线段AB上时,M点到AB两点距离之和的最小值为AB的长;
(3)用AB的长度除以点Q与点P的速度差即可得解;
(4)分析M点在不同的位置时,所得到的M的值即可.
(1)∵a是最大的负整数,
∴a=﹣1,
∵b是多项式2m2n﹣m3n2﹣m﹣2的次数,
∴b=3+2=5,
∵c是单项式﹣2xy2的系数,
∴c=﹣2,
如图所示:
![]()
(2)当M点在线段AB上时,M点到AB两点距离之和的最小值为5﹣(﹣1)=6;
(3)∵动点P、Q同时从A、B出发沿数轴负方向运动,点P的速度是每秒![]() 个单位长度,
个单位长度,
点Q的速度是每秒2个单位长度,
∴AB=6,两点速度差为:2﹣![]() ,
,
∴6÷(2﹣![]() )=4,
)=4,
答:运动4秒后,点Q可以追上点P;
(4)存在点M,使P到A、B、C的距离和等于10,
当M在AB之间,则M对应的数是2,
当M在C点左侧,则M对应的数是:﹣2![]() .
.
综上所述,M对应的数为2或﹣2![]() .
.
-
科目: 来源: 题型:
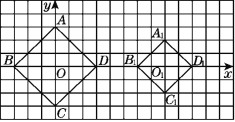
查看答案和解析>>【题目】如图,正方形ABCD和正方形A1B1C1D1的对角线(正方形相对顶点之间所连的线段)BD,B1D1都在x轴上,O,O1分别为正方形ABCD和正方形A1B1C1D1的中心(正方形对角线的交点称为正方形的中心),O为平面直角坐标系的原点.OD=3,O1D1=2.
(1)如果O1在x轴上平移时,正方形A1B1C1D1也随之平移,其形状、大小没有改变,当中心O1在x轴上平移到两个正方形只有一个公共点时,求此时正方形A1B1C1D1各顶点的坐标;
(2)如果O在x轴上平移时,正方形ABCD也随之平移,其形状、大小没有改变,当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时,求此时正方形ABCD各顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①在数轴上没有点能表示
 +1;②无理数是开不尽方的数;③存在最小的实数;④4的平方根是±2,用式子表示是
+1;②无理数是开不尽方的数;③存在最小的实数;④4的平方根是±2,用式子表示是 =±2;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中正确的是______.
=±2;⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0,其中正确的是______. -
科目: 来源: 题型:
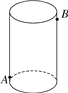
查看答案和解析>>【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
收费
方式
月使用费(元)
包时上网
时间(h)
超时费(元/min)
A
7
25
0.6
B
10
50
0.8
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,点E在BC边上,且CE=2,AE与BD交于点F,连接CF,则下列结论不正确的是( )
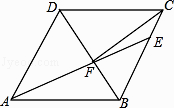
A.△ABF≌△CBF
B.△ADF∽△EBF
C.tan∠EAB=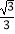
D.S△EAB=6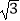
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某运算程序,该程序是循环迭代的一种.根据该程序的指令,如果输入
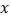 的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )
的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )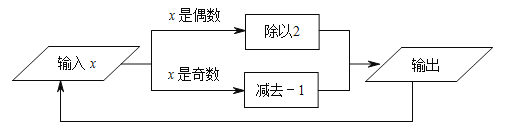
A. 4 B. 3 C. 2 D. 1
相关试题

