【题目】如图,矩形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm,当沿AE折叠时,顶点D落在BC边上的点F处,试求CE的长.

参考答案:
【答案】3
【解析】试题分析:由折叠的性质得AF=AD=10cm,DE=EF,先在Rt△ABF中运用勾股定理求BF,再求CF,设CE=xcm,用含x的式子表示FE,在Rt△CEF中运用勾股定理列方程求x即可.
试题解析:(6分)解:∵四边形ABCD为矩形,
∴AD=BC=10,DC=AB=8,∠B=∠C=90°.
∵△AEF由△ADE沿AE折叠而成,
∴(由轴对称的性质得)AF=AD=10,FE=DE.
在Rt△ABF中,有AB2+BF2=AF2,即82+BF2=102,
得BF=6,∴CF=BC-BF=10-6=4.
设CE=![]() ,则FE=DE=
,则FE=DE=![]() ,
,
在Rt△CEF中,有CF2+CE2=EF2,即42+![]() 2=
2=![]() .
.
∴![]() =3,∴CE的长为3cm.
=3,∴CE的长为3cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,
 的顶点都在网格点上,其中,C点坐标为
的顶点都在网格点上,其中,C点坐标为 .
. 填空:点A的坐标是______,点B的坐标是______;
填空:点A的坐标是______,点B的坐标是______; 将
将 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到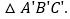 请写出
请写出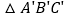 的三个顶点坐标;
的三个顶点坐标; 求
求 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,△ABC的顶点和点O均在网格图的格点上,将△ABC绕点O逆时针旋转90°,得到△A1B1C1 .

(1)请画出△A1B1C1;
(2)以点O为圆心, 为半径作⊙O,请判断直线AA1与⊙O的位置关系,并说明理由.
为半径作⊙O,请判断直线AA1与⊙O的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 ,直线
,直线 ;直线
;直线 分别交
分别交 轴于
轴于 两点,
两点, 相交于点
相交于点 .
.⑴求
 三点的坐标;
三点的坐标;⑵求⊿
 的面积.
的面积. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,E为BC中点,AE⊥BC于点E,AF⊥CD于点F,CG∥AE,CG交AF于点H,交AD于点G.
(1)求菱形ABCD的面积;(2)求∠CHA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为加强学生的体育锻炼,曾两次在某商场购买足球和篮球
 第一次购买6个足球和5个篮球共花费700元;第二次购买3个足球和7个篮球共花费710元.
第一次购买6个足球和5个篮球共花费700元;第二次购买3个足球和7个篮球共花费710元. 求足球和篮球的标价;
求足球和篮球的标价; 如果现在商场均以标价的6折对足球和篮球进行促销,学校决定从该商场再一次性购买足球和篮球60个,且总费用不能超过2500元,那么最多可以购买多少个篮球?
如果现在商场均以标价的6折对足球和篮球进行促销,学校决定从该商场再一次性购买足球和篮球60个,且总费用不能超过2500元,那么最多可以购买多少个篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,
证明你的结论.
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形;
(3)当四边形ABCD的对角线满足_____条件时,四边形EFGH是菱形;
(4)你学过的哪种特殊四边形的中点四边形是矩形?_____;
(5)你学过的哪种特殊四边形的中点四边形是菱形?_____;
(6)你学过的哪种特殊四边形的中点四边形是正方形?_____.

相关试题

