【题目】三角形中的角平分线的性质与一个角的平分线性质相同.如题:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.请你结合条件认真研究,然后写出三个正确的结论.
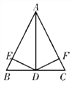
参考答案:
【答案】如:(1)△BDE≌△CDF,(2)BE=CF,(3)∠B=∠C.
【解析】试题分析:此题答案不唯一,如先利用角平分线的性质,可得DE=DF;在Rt△BDE和Rt△CDF中,再结合已知条件,可证出Rt△BDE≌Rt△CDF,那么就有BE=CF,∠B=∠C.
解:答案不唯一,如:(1)△BDE≌△CDF;(2)BE=CF;(3)∠B=∠C.
证明:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
又∵BD=CD,
∴Rt△BDE≌Rt△CDF,
∴BE=CF,∠B=∠C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,M,N分别是OA,OB边上的点,点P在射线OC上,则下列条件中不能说明OC平分∠AOB的是( )
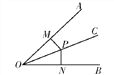
A. PM⊥OA,PN⊥OB,PM=PN B. PM=PN,OM=ON
C. PM⊥OA,PN⊥OB,OM=ON D. PM=PN,∠PMO=∠PNO
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等.
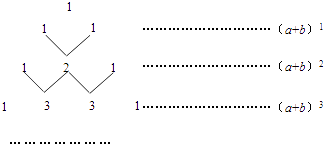
(1)根据上面的规律,则(a+b)5的展开式= .
(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x>y,则下列不等式成立的是( )
A.x﹣1<y﹣1
B.3x<3y
C.﹣x<﹣y
D.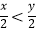
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2a2﹣8b2=
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a为方程x2﹣x﹣1=0的一个根,则代数式a4﹣2a2﹣a=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?

相关试题

