【题目】阅读下面材料并回答问题:
点A,B在数轴上分别表示数a,b,A,B两点之间的距离表示为AB.
当A,B两点中有一点在原点时:
不妨设A在原点,如图1,AB=OB=|b|=|a-b|;
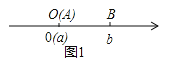
当A,B两点都不在原点时:
①如图2,点A,B都在原点的右边,AB=OB-OA=|b|-|a|=b-a=|a-b|;
![]()
②如图3,点A,B都在原点左边,AB=OB-OA=|b|-|a|=(-b)-(-a)=|a-b|;

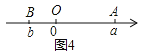
③如图4,点A,B在原点的两边,AB=OA+OB=|a|+|b|=a+(-b)=|a-b|;
综上,数轴上A,B两点之间的距离AB=|a-b|.
(1)回答问题:数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ,数轴上表示x和-1的两点之间的距离是 .
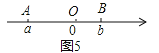
(2)如图5,若|a-b|=2013,且OA=2OB,求a+b的值.
(3)结合两点之间的距离,若点M表示的数为x,当代数式|x+1|+|x-2|取最小值时,相应x的取值范围是
参考答案:
【答案】(1)3,3,4,|x+1|;(2)-671;(3)-1≤x≤2.
【解析】试题分析:(1)根据两点间的距离公式即可求解;
(2)根据题意列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值;
的值;
(3)当![]() 大于等于0,且
大于等于0,且![]() 小于等于0时,原式取得最小值,求出这个最小值即可.
小于等于0时,原式取得最小值,求出这个最小值即可.
试题解析:(1)数轴上表示2和5的两点之间的距离是52=3,数轴上表示2和5的两点之间的距离是2(5)=3,数轴上表示1和3的两点之间的距离是1(3)=4,数轴上表示x和1的两点之间的距离是|x+1|.
(2)∵|ab|=2013,且OA=2OB,
∴3b=2013,解得b=671,
a=2b=1342,
a+b=1342+671=671.
故a+b的值是671.
(3)数形结合,若|x+1|+|x2|取最小值,那么表示x的点M在1和2之间的线段上,
所以![]()
故答案为:3,3,4,|x+1|; ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】将线段AB向右平移3cm,得到线段CD,如果AB=5cm,则CD=______,BD=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
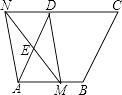
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为时,四边形AMDN是矩形; ②当AM的值为时,四边形AMDN是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD的对角线BD上的一点,且BE=BC,AB=3,BC=4,点P为直线EC上的一点,且PQ⊥BC于点Q,PR⊥BD于点R.
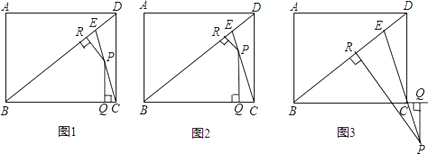
(1)①如图1,当点P为线段EC中点时,易证:PR+PQ=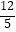 (不需证明). ②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(不需证明). ②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(2)如图3,当点P为线段EC延长线上的任意一点时,其它条件不变,则PR与PQ之间又具有怎样的数量关系?请直接写出你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE=AE,则边BC的长为( )
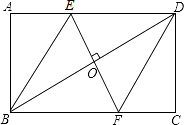
A.2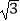
B.3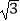
C.
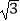
D.6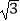
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于多项式22m2+3m﹣1,下列说法正确的是( )
A.它是关于m的四次三项式
B.它的常数项是1
C.它是按m的降幂排列
D.它是按m的升幂排列 -
科目: 来源: 题型:
查看答案和解析>>【题目】画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得2BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
相关试题

