【题目】画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得2BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
参考答案:
【答案】(1)画图见解析;(2)点A,AB=![]() CD;(3)5cm.
CD;(3)5cm.
【解析】试题分析:
(1) 先画出长度为2cm的线段AB,再沿点A到点B的方向延长线段AB至点C,使得BC=1cm. 然后,沿点C到点A的方向延长线段AC至点D,使得AD=3cm. 这样得到的图形即为所求.
(2) 根据AD=AC和线段中点的定义,易知点A是线段DC的中点. 根据2BC=AB,可以求得线段AB与线段AC的长度关系,再根据AD=AC即可求得线段AB与线段DC的长度关系.
(3) 要求线段BD的长,只要求得线段AD的长即可. 根据2BC=AB和线段AB的长,可以求得线段BC的长,从而易得线段AC的长. 根据AD=AC,易知线段AD的长. 根据BD=AD+AB即可得到线段BD的长.
试题解析:
(1) 根据题意可画出如下图形.
![]()
(2) 因为AD=AC,所以点A是线段DC的中点.
因为2BC=AB,所以![]() .
.
因为AD=AC,所以![]() .
.
因此, ![]() .
.
答:线段DC的中点是点A. 线段AB的长是线段DC长的三分之一.
(3) 因为2BC=AB,AB=2cm,所以![]() (cm).
(cm).
故AC=AB+BC=2+1=3(cm).
因为AD=AC,所以AD=AC=3(cm).
因此,BD=AD+AB=3+2=5(cm),即线段BD的长度为5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:
 .
.该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故
 ,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证.
,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证.(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正数的平方根分别是2a﹣7与﹣a+2,求这个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较下列四个算式结果的大小(在横线上填“>”“<”或“=”).
(1)42+52_______2×4×5;
(2)(-1)2+22_______2×(-1)×2;
(3)(-3)2+
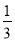 2______2×(-3)×
2______2×(-3)×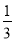 ;
;(4)32+32_______2×3×3;
(5)请通过观察归纳,写出反映这种规律的一般结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:
 ≈1.4,
≈1.4, ≈1.7).
≈1.7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)(x-2)(x+3)=-4 (公式法) (2)2x2+4x+1=25(配方法)
(3)3(x-5)2=x-5 (4)(x+3)2=(3x-5)2.
相关试题

