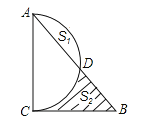
【题目】以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
参考答案:
【答案】(1)证明见解析;(2)S2-S1=-![]() x2+4x;(3)BD=
x2+4x;(3)BD=![]() .
.
【解析】
(1)由抛物线的顶点在![]() 轴上,得到
轴上,得到![]() 从而可得结论.
从而可得结论.
(2)利用a是z2+z-20=0的根,求解![]() 的值,再利用S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆,从而可得答案,
的值,再利用S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆,从而可得答案,
(3)由(2)的函数关系式求解(![]() )最大时
)最大时![]() ,利用直径所对的圆周角是直角,得到
,利用直径所对的圆周角是直角,得到![]() 利用相似三角形的性质可得答案.
利用相似三角形的性质可得答案.
(1)因为二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)的顶点在x轴上,
(c-a)的顶点在x轴上,
∴ Δ=0,即:b2-4×![]() (a+c)×
(a+c)×![]() (c-a)=0,
(c-a)=0,
∴ c2=a2+b2,
得∠ACB=90°.
(2)∵ z2+z-20=0.
∴ z1=-5,z2=4,
∵ a>0,得a=4.
设b=AC=2x,有S△ABC=![]() AC·BC=4x,S半圆=
AC·BC=4x,S半圆=![]() x2
x2
∴ S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆=-![]() x2+4x
x2+4x
(3)![]() S2-S1=-
S2-S1=-(x-
![]() )2+
)2+![]() ,
,
∴ 当x=![]() 时,(S2-S1)有最大值
时,(S2-S1)有最大值![]() .
.
这时,b=![]() ,a=4,c=
,a=4,c=![]() ,
,
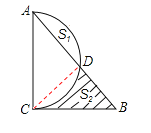
如图,连接![]()
![]() 为圆的直径,
为圆的直径,
![]()
![]()
![]()
![]()
![]() BD=
BD=![]() .
.
当BD为![]() 时,(S2-S1)最大.
时,(S2-S1)最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】声音在空气中传播的速度y(米/秒)是气温x (摄氏度)的一次函数,下表列出了一组不同气温时的音速.
气温x/摄氏度
0
5
10
15
20
音速y/(米/秒)
331
334
337
340
343
(1)求y 与 x之间的函数关系式
(2)气温x=22(摄氏度)时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地相距多远?
-
科目: 来源: 题型:
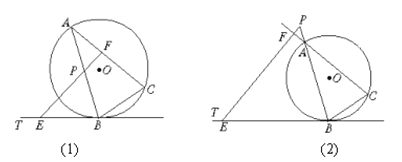
查看答案和解析>>【题目】已知:△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过P作BC的平行线交直线BT于点E,交直线AC于点F.
(1)如图 (1)所示,当P在线段AB上时,求证:PA·PB=PE·PF;
(2)如图 (2)所示,当P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先仔细阅读下列材料,然后回答问题:
如果a>0,b>0,那么(
 -
- )2≥0,即a+b-2
)2≥0,即a+b-2 ≥0 得
≥0 得 ≥
≥ ,其中,当a=b时取等号,我们把
,其中,当a=b时取等号,我们把 称为a、b的算术平均数,
称为a、b的算术平均数,  称为a、b的几何平均数.
称为a、b的几何平均数.如果a>0,b>0,c>0,同样可以得到
 ≥
≥ ,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)
,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)(1)设剪去的小正方形边长为x cm,无盖纸盒的容积为V,求V与x的函数关系式及x的取值范围.
(2)当x为何值时,容积V有最大值,最大值是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于题目:在平面直角坐标系中,直线
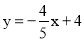 分别与
分别与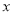 轴、
轴、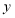 轴交于
轴交于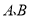 两点,过点
两点,过点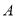 且平行
且平行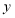 轴的直线与过点
轴的直线与过点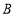 且平行
且平行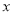 轴的直线相交于点
轴的直线相交于点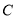 ,若抛物线
,若抛物线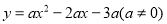 与线段
与线段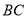 有唯一公共点,求
有唯一公共点,求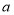 的取值范围.甲的计算结果是
的取值范围.甲的计算结果是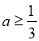 ;乙的计算结果是
;乙的计算结果是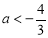 ,则( )
,则( )A.甲的结果正确B.乙的结果正确
C.甲与乙的结果合在一起正确D.甲与乙的结果合在一起也不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过正六边形
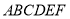 的顶点
的顶点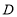 作一条直线
作一条直线 于点
于点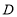 ,分别延长
,分别延长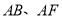 交直线
交直线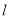 于点
于点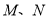 ,则
,则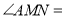 ___;若正六边形
___;若正六边形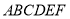 的面积为
的面积为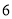 ,则
,则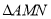 的面积为__.
的面积为__.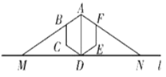
-
科目: 来源: 题型:
查看答案和解析>>【题目】在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在
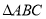 中,
中,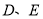 分别是边
分别是边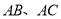 的中点.
的中点.求证: .
证明:如图,延长
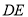 到点
到点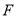 ,使
,使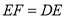 ,连接
,连接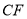 ,
,···
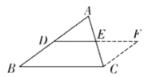
(1)补全求证:
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若
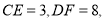 求边
求边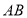 的取值范围.
的取值范围.
相关试题

