【题目】如图,过正六边形![]() 的顶点
的顶点![]() 作一条直线
作一条直线![]() 于点
于点![]() ,分别延长
,分别延长![]() 交直线
交直线![]() 于点
于点![]() ,则
,则![]() ___;若正六边形
___;若正六边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为__.
的面积为__.
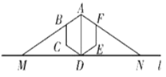
参考答案:
【答案】![]()
![]()
【解析】
因为正六边形每个内角都是120![]() ,AD⊥MN,且平分∠BAF,在直角三角形AMD中即可求得∠AMN=30
,AD⊥MN,且平分∠BAF,在直角三角形AMD中即可求得∠AMN=30![]() ;作出辅助线,利用特殊角以及三角形全等,可证得
;作出辅助线,利用特殊角以及三角形全等,可证得![]() =8,同理可得:
=8,同理可得:![]() =8,最终即可求得
=8,最终即可求得![]() =
=![]() +
+![]() =8+8=16.
=8+8=16.
如图,连接BECF相交于O,延长DC交AM于P,延长DE交AN于Q,
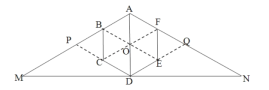
∵正六边形ABCDEF,
∴∠BAF=∠ABC=∠BCD=120![]() ,
,
∵AD是正六边形ABCDEF的对角线,
∴∠BAD=![]() ∠BAF=60
∠BAF=60![]() ,
,
∵AD⊥MN,∠ADM=90![]() ,
,
∴∠AMN=30![]()
∴![]() =
=![]() =
=![]() ,
,
∴∠PBC=∠PCB=60![]() ,
,
∴△PBC是等边三角形,
∴PB=PC=BC,
∵正六边形ABCDEF,
∴△ABO是等边三角形,AB=BC,
∴AB=OB=OA,
∴AB=OA=OB=BC=PB=PC,
∴△ABO![]() △BCP(SSS) ,
△BCP(SSS) ,
∴![]() =
=![]() =1,
=1,
∴![]() =4,
=4,
在Rt△ADM中,∠AMD=30![]() ,
,
∴AM=2AD=4AB=2AP,
∴![]() =8,
=8,
同理可得:![]() =8,
=8,
∴![]() =
=![]() +
+![]() =8+8=16.
=8+8=16.
故答案为:30![]() ,16.
,16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先仔细阅读下列材料,然后回答问题:
如果a>0,b>0,那么(
 -
- )2≥0,即a+b-2
)2≥0,即a+b-2 ≥0 得
≥0 得 ≥
≥ ,其中,当a=b时取等号,我们把
,其中,当a=b时取等号,我们把 称为a、b的算术平均数,
称为a、b的算术平均数,  称为a、b的几何平均数.
称为a、b的几何平均数.如果a>0,b>0,c>0,同样可以得到
 ≥
≥ ,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)
,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)(1)设剪去的小正方形边长为x cm,无盖纸盒的容积为V,求V与x的函数关系式及x的取值范围.
(2)当x为何值时,容积V有最大值,最大值是多少?

-
科目: 来源: 题型:
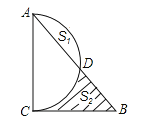
查看答案和解析>>【题目】以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y=
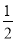 (a+c)x2-bx+
(a+c)x2-bx+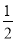 (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(c-a)顶点在x轴上,a是方程z2+z-20=0的根.(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于题目:在平面直角坐标系中,直线
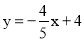 分别与
分别与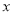 轴、
轴、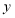 轴交于
轴交于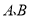 两点,过点
两点,过点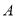 且平行
且平行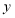 轴的直线与过点
轴的直线与过点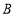 且平行
且平行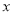 轴的直线相交于点
轴的直线相交于点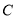 ,若抛物线
,若抛物线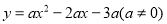 与线段
与线段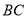 有唯一公共点,求
有唯一公共点,求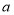 的取值范围.甲的计算结果是
的取值范围.甲的计算结果是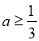 ;乙的计算结果是
;乙的计算结果是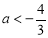 ,则( )
,则( )A.甲的结果正确B.乙的结果正确
C.甲与乙的结果合在一起正确D.甲与乙的结果合在一起也不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在
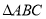 中,
中,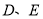 分别是边
分别是边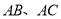 的中点.
的中点.求证: .
证明:如图,延长
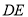 到点
到点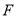 ,使
,使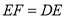 ,连接
,连接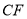 ,
,···
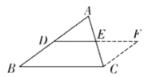
(1)补全求证:
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若
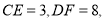 求边
求边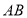 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2).
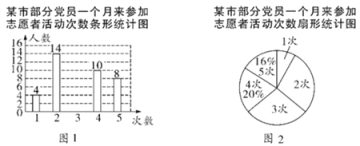
(1) “
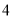 次”所在扇形的圆心角度数是 ,请补全 条形统计图;
次”所在扇形的圆心角度数是 ,请补全 条形统计图;(2)若从抽在的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于
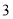 次的概率;
次的概率;(3)设随机抽查的党员一个月来参加志愿者活动次数的中位数为
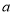 ,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为
,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为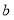 ,当
,当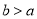 时,求最少去掉了几名党员参加志愿者活动的次数.
时,求最少去掉了几名党员参加志愿者活动的次数. -
科目: 来源: 题型:
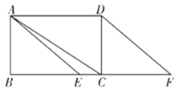
查看答案和解析>>【题目】如图,在矩形
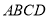 中,点
中,点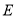 是边
是边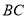 上一点(不与点
上一点(不与点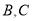 重合),点
重合),点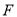 是
是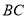 延长线上一点,且
延长线上一点,且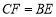 ,连接
,连接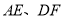 .
.
(1)求证:
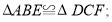
(2)连接
 ,其中
,其中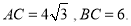
①当四边形
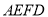 是菱形时,求线段
是菱形时,求线段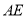 与线段
与线段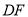 之间的距离;
之间的距离;②若点
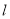 是
是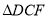 的内心,连接
的内心,连接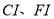 ,直接写出
,直接写出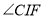 的取值范围.
的取值范围.
相关试题

