【题目】如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于( ) 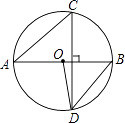
A.40°,80°
B.50°,100°
C.50°,80°
D.40°,100°
参考答案:
【答案】B
【解析】解:∵CD⊥AB,
∴∠AEC=90°,
∵∠CAB=40°,
∴∠C=50°,
∴∠ABD=∠C=50°,
∵OB=OD,
∴∠ABD=∠ODB=50°,
∴∠AOD=∠ABD+∠ODB=100°,
故选B.
求出∠AEC=90°,根据三角形内角和定理求出∠C=50°,根据圆周角定理即可求出∠ABD,根据OB=OD得出∠ABD=∠ODB=50°,根据三角形外角性质求出即可.本题考查了圆周角定理,垂径定理的应用,能熟记圆周角定理的内容是解此题的关键.
-
科目: 来源: 题型:
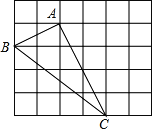
查看答案和解析>>【题目】如图,在由边长为1的小正方形组成的5×6的网格中,△ABC的三个顶点均在格点上,请按要求解决下列问题:
(1)通过计算判断△ABC的形状;
(2)在图中确定一个格点D,连接AD、CD,使四边形ABCD为平行四边形,并求出 □ABCD的面积.
-
科目: 来源: 题型:
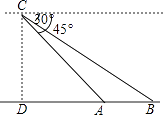
查看答案和解析>>【题目】如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m的高空C处时,测得A处渔政船的俯角为45°,测得B处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB是( )
A.3000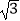 m
m
B.3000(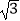 +1)m
+1)m
C.3000(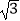 -1)m
-1)m
D.1500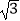 m
m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E为ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则ABCD的面积为( )
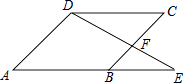
A.30
B.27
C.14
D.32 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2﹣
 x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.
相关试题

