【题目】已知矩形![]() 和点
和点![]() ,当点
,当点![]() 在
在![]() 上任一位置(如图
上任一位置(如图![]() 所示)时,易证得结论:
所示)时,易证得结论:![]() ,请你探究:当点
,请你探究:当点![]() 分别在图
分别在图![]() 、图
、图![]() 中的位置时,
中的位置时,![]() 、
、![]() 、
、![]() 和
和![]() 又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图
又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图![]() 证明你的结论.
证明你的结论.
答:对图![]() 的探究结论为________;
的探究结论为________;
对图![]() 的探究结论为________;
的探究结论为________;
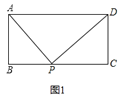


参考答案:
【答案】![]()
![]()
【解析】
结论均是:![]() .如图2,过点P作MN∥AB,交AD于点M,交BC于点N,可得四边形ABNM和四边形NCDM均为矩形,根据(1)中的结论可得,在矩形ABNM中有PA2+PN2=PB2+PM2①,在矩形NCDM中有PC2+PM2=PD2+PN2②, 利用①+②即可证得结论;如图3,过点P作MN∥AB,交AB的延长线于点M,交CD的延长线于点N,用上面的方法解决即可.
.如图2,过点P作MN∥AB,交AD于点M,交BC于点N,可得四边形ABNM和四边形NCDM均为矩形,根据(1)中的结论可得,在矩形ABNM中有PA2+PN2=PB2+PM2①,在矩形NCDM中有PC2+PM2=PD2+PN2②, 利用①+②即可证得结论;如图3,过点P作MN∥AB,交AB的延长线于点M,交CD的延长线于点N,用上面的方法解决即可.
结论均是:![]() .
.
(1)如图2,过点P作MN∥AB,交AD于点M,交BC于点N,
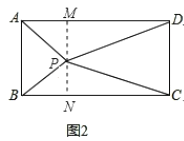
∴四边形ABNM和四边形NCDM均为矩形,
根据(1)中的结论可得,
在矩形ABNM中可得:PA2+PN2=PB2+PM2①,
在矩形NCDM中可得:PC2+PM2=PD2+PN2②,
①+②得:PA2+PN2+PC2+PM2=PB2+PM2+PD2+PN2,
∴PA2+PC2=PB2+PD2.
(2)如图3,过点P作MN∥AB,交AB的延长线于点M,交CD的延长线于点N,
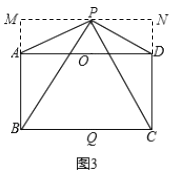
∴四边形BCNM和四边形ADNM均为矩形,
同样根据(1)中的结论可得,
在矩形BCNM中可得:PC2+PM2=PB2+PN2①,
在矩形ADNM中可得:PA2+PN2=PD2+PM2②,
①+②得:PA2+PN2+PC2+PM2=PD2+PM2+PB2+PN2,
∴PA2+PC2=PB2+PD2.
故答案为: ![]() ;
; ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 在
在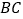 上过点
上过点 分别作
分别作 、
、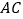 的平行线,分别交
的平行线,分别交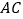 、
、 于点
于点 、
、
①如果要得到矩形
 ,那么
,那么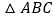 应具备条件:________;
应具备条件:________;②如果要得到菱形
 ,那么
,那么 应具备条件:________.
应具备条件:________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点
 是正方形
是正方形 的对角线
的对角线 上一点,
上一点, 于
于 ,
, 于
于 ,连接
,连接 ,给出下列四个结论:
,给出下列四个结论:①
 ;②
;② 一定是等腰三角形;③
一定是等腰三角形;③ ;④
;④ ,
,其中正确结论的序号是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:
问题:如图,在正方形
 和平行四边形
和平行四边形 中,点
中,点 ,
, ,
, 在同一条直线上,
在同一条直线上, 是线段
是线段 的中点,连接
的中点,连接 ,
, .
.探究:当
 与
与 的夹角为多少度时,平行四边形
的夹角为多少度时,平行四边形 是正方形?
是正方形?小聪同学的思路是:首先可以说明四边形
 是矩形;然后延长
是矩形;然后延长 交
交 于点
于点 ,构造全等三角形,经过推理可以探索出问题的答案.
,构造全等三角形,经过推理可以探索出问题的答案.请你参考小聪同学的思路,探究并解决这个问题.

(1)求证:四边形
 是矩形;
是矩形;(2)
 与
与 的夹角为________度时,四边形
的夹角为________度时,四边形 是正方形.
是正方形.理由:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2
 , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )
A. 2
 B. 4 C. 4
B. 4 C. 4 D. 8
D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )

A. 4B. 4.6C. 4.8D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别为AB、BC上的点,且AE=BF,连结DE、AF,猜想DE、AF的关系并证明.

相关试题

