【题目】如图所示,点![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上一点,
上一点,![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() ,给出下列四个结论:
,给出下列四个结论:
①![]() ;②
;②![]() 一定是等腰三角形;③
一定是等腰三角形;③![]() ;④
;④![]() ,
,
其中正确结论的序号是________.

参考答案:
【答案】①③④
【解析】
连接PC,根据正方形的对角线平分一组对角可得∠ABP=∠CBP=45°,然后利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,对应角相等可得∠BAP=∠BCP,再根据矩形的对角线相等可得EF=PC,对边相等可得PF=EC,再判断出△PDF是等腰直角三角形,然后根据等腰直角三角形的斜边等于直角边的![]() 倍解答即可.
倍解答即可.
如图,连接PC,
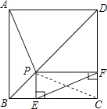
在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
∵在△ABP和△CBP中,
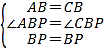
∴△ABP≌△CBP(SAS),
∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF是矩形,
∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
∵PF⊥CD,∠BDC=45°,
∴△PDF是等腰直角三角形,
∴PD=![]() PF,
PF,
又∵矩形的对边PF=EC,
∴PD=![]() EC,故④正确;
EC,故④正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
综上所述,正确的结论有①③④.
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
 的正方形
的正方形 的对角线交于点
的对角线交于点 ,把边
,把边 、
、 分别绕点
分别绕点 、
、 同时逆时针旋转
同时逆时针旋转 得四边形
得四边形 ,其对角线交点为
,其对角线交点为 ,连接
,连接 .下列结论:
.下列结论:
①四边形
 为菱形;
为菱形;②
 ;
;③线段
 的长为
的长为 ;
;④点
 运动到点
运动到点 的路径是线段
的路径是线段 .其中正确的结论共有( )
.其中正确的结论共有( )A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一刻度尺检验一个四边形是否为矩形,以下方法可行的有________.(只要填序号即可)
①量出四边及两条对角线,比较对边是否相等,对角线是否相等.
②量出对角线的交点到四个顶点的距离,看是否相等.
③量出一组邻边的长
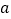 、
、 以及和这两边组成三角形的那条对角线的长
以及和这两边组成三角形的那条对角线的长 ,计算是否有
,计算是否有 .
.④量出两条对角线长,看是否相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
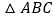 中,点
中,点 在
在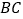 上过点
上过点 分别作
分别作 、
、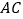 的平行线,分别交
的平行线,分别交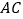 、
、 于点
于点 、
、
①如果要得到矩形
 ,那么
,那么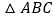 应具备条件:________;
应具备条件:________;②如果要得到菱形
 ,那么
,那么 应具备条件:________.
应具备条件:________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:
问题:如图,在正方形
 和平行四边形
和平行四边形 中,点
中,点 ,
, ,
, 在同一条直线上,
在同一条直线上, 是线段
是线段 的中点,连接
的中点,连接 ,
, .
.探究:当
 与
与 的夹角为多少度时,平行四边形
的夹角为多少度时,平行四边形 是正方形?
是正方形?小聪同学的思路是:首先可以说明四边形
 是矩形;然后延长
是矩形;然后延长 交
交 于点
于点 ,构造全等三角形,经过推理可以探索出问题的答案.
,构造全等三角形,经过推理可以探索出问题的答案.请你参考小聪同学的思路,探究并解决这个问题.

(1)求证:四边形
 是矩形;
是矩形;(2)
 与
与 的夹角为________度时,四边形
的夹角为________度时,四边形 是正方形.
是正方形.理由:
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形
 和点
和点 ,当点
,当点 在
在 上任一位置(如图
上任一位置(如图 所示)时,易证得结论:
所示)时,易证得结论: ,请你探究:当点
,请你探究:当点 分别在图
分别在图 、图
、图 中的位置时,
中的位置时, 、
、 、
、 和
和 又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图
又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图 证明你的结论.
证明你的结论.答:对图
 的探究结论为________;
的探究结论为________;对图
 的探究结论为________;
的探究结论为________;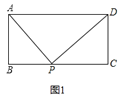


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2
 , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )
A. 2
 B. 4 C. 4
B. 4 C. 4 D. 8
D. 8
相关试题

