Question

【题目】直线AB、CD相交于点O，OE平分∠BOD，OF⊥CD，垂足为O．

（1）若∠EOF=54°，求∠AOC的度数；

（2）①在∠AOD的内部作射线OG⊥OE；

②试探索∠AOG与∠EOF之间有怎样的关系？并说明理由．

Answer 1

【答案】（1）∠AOC=72°；（2）∠AOG=∠EOF

【解析】试题分析：（1）利用角平分线的性质结合已知得出∠DOE的度数，进而得出答案；

（2）①根据要求作图即可；

②由OG⊥OE得∠AOG+∠GOE+∠BOE=180°,由OF⊥CD得∠COF+∠FOE+∠DOE= 180°,又OE是角平分线，即可得出结论.

试题解析：（1）∵OE平分∠BOD，

∴∠BOE=∠DOE，

∵∠EOF=54°，OD⊥OF，

∴∠DOE=36°，

∴∠BOE=36°，

∴∠AOC=72°；

（2）①如图所示，

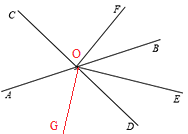
②∵OF⊥CD,

∴∠COF=90°，∠COF+∠EOF+∠EOD=180°，

∵OG⊥OE

∴∠GOE=90°，∠AOG+∠GOE+∠EOB=180°

∵OE平分∠BOD，

∴∠BOE=∠DOE，

∴∠AOG=∠EOF.