【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
参考答案:
【答案】A
【解析】
根据等腰三角形三线合一的性质可得AP=PD,然后根据等底等高的三角形面积相等求出△BPC的面积等于△ABC面积的一半,代入数据计算即可得解.
∵BD=BA,BP是∠ABC的平分线,
∴AP=PD,
∴S△BPD=![]() S△ABD,S△CPD=
S△ABD,S△CPD=![]() S△ACD,
S△ACD,
∴S△BPC=S△BPD+S△CPD=![]() S△ABD+
S△ABD+![]() S△ACD=
S△ACD=![]() S△ABC,
S△ABC,
∵△ABC的面积为8cm2,
∴S△BPC=![]() ×8=4cm2,
×8=4cm2,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
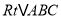 中,
中,  ,
,  ,
, 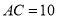 ,
,  和
和 的平分线相交于点E,过点E作
的平分线相交于点E,过点E作 交
交 于点F,那么EF的长为( )
于点F,那么EF的长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
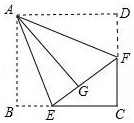
A.1.5
B.2.5
C.2.25
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.P是直径MN上一动点,则PA+PB的最小值为( )
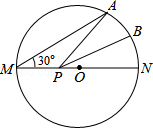
A.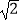
B.1
C.2
D.2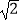
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论: ①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有三个点A,B,C,表示的数分别是﹣4,﹣2,3.
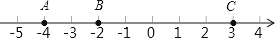
(1)若使C、B两点的距离是A、B两点的距离的2倍,则需将点C向左移动 个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒a个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒:
①点A、B、C表示的数分别是 、 、 (用含a、t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当a为何值时,5d1﹣3d2的值不会随着时间t的变化而改变,并求此时5d1﹣3d2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=
 ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?
相关试题

