【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

参考答案:
【答案】(1)30;(2)答案见解析;(3)65°或52.5°.
【解析】试题分析:(1)根据图形得出∠COE=∠BOE-∠COB,代入求出即可;
(2)根据角平分线定义求出∠COE=∠AOE=![]() ∠COA,再根据∠AOE+∠DOB=90°,∠COE+∠COD=90°,可得∠COD=∠DOB,从而问题得证;
∠COA,再根据∠AOE+∠DOB=90°,∠COE+∠COD=90°,可得∠COD=∠DOB,从而问题得证;
(3)设∠COD=x°,则∠AOE=5x°,根据题意则可得6x=30或5x+90﹣x=120,解方程即可得.
试题解析:(1)∵∠BOE=∠COE+∠COB=90°,
又∵∠COB=60°,
∴∠COE=∠BOE-∠COB=30°,
故答案为:30;
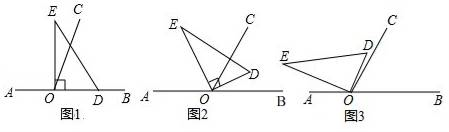
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=![]() ∠COA,
∠COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB,
∴OD所在射线是∠BOC的平分线;
(3)设∠COD=x°,则∠AOE=5x°,
∵∠DOE=90°,∠BOC=60°,
∴6x=30或5x+90﹣x=120,
∴x=5或7.5,
即∠COD=65°或37.5°,
∴∠BOD=65°或52.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论: ①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有三个点A,B,C,表示的数分别是﹣4,﹣2,3.
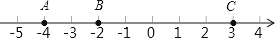
(1)若使C、B两点的距离是A、B两点的距离的2倍,则需将点C向左移动 个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒a个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒:
①点A、B、C表示的数分别是 、 、 (用含a、t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当a为何值时,5d1﹣3d2的值不会随着时间t的变化而改变,并求此时5d1﹣3d2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣2﹣6sin30°﹣(
)﹣2﹣6sin30°﹣( 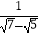 )0+
)0+ 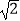 +|
+| 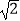 ﹣
﹣ 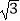 |
| -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把成绩结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
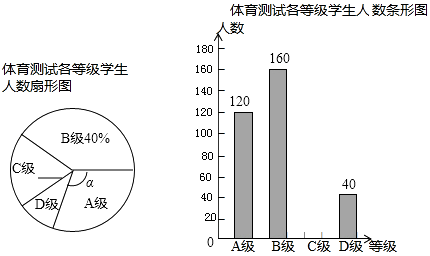
(1)求本次抽样测试的学生人数;
(2)求扇形图中∠α的度数,并把条形统计图补充完整;
(3)该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
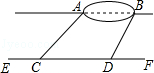
相关试题

