【题目】已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。

求证:(1)△ADF≌△CBE
(2)EB∥DF.
参考答案:
【答案】∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC. ………………(1分)
∴∠DAC=∠BCE.
又∵AE=CF,∴AF=CE
∴△ADF≌△CBE.……………………(4分)
∴∠AFD=∠CEB.
∴BE∥DF. ……………………………(6分
【解析】试题分析:要证△ADF≌△CBE,因为AE=CF,则两边同时加上EF,得到AF=CE,又因为ABCD是平行四边形,得出AD=CB,∠DAF=∠BCE,从而根据SAS推出两三角形全等,由全等可得到∠DFA=∠BEC,所以得到DF∥EB.
证明:(1)∵AE=CF,
∴AE+EF=CF+FE,即AF=CE.
又ABCD是平行四边形,
∴AD=CB,AD∥BC.
∴∠DAF=∠BCE.
在△ADF与△CBE中![]() ,
,
∴△ADF≌△CBE(SAS).
(2)∵△ADF≌△CBE,
∴∠DFA=∠BEC.
∴DF∥EB.
-
科目: 来源: 题型:
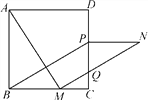
查看答案和解析>>【题目】如图,在正方形ABCD中,点M是BC边上的任一点,连结AM并将线段AM绕点M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连结NP、BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连结AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合.三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,请直接写出
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.

-
科目: 来源: 题型:
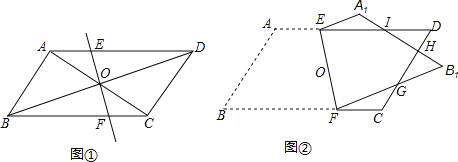
查看答案和解析>>【题目】(1)如图①,ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.
(2)如图②,将ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
-
科目: 来源: 题型:
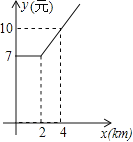
查看答案和解析>>【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
-
科目: 来源: 题型:
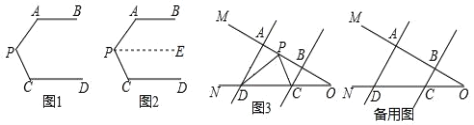
查看答案和解析>>【题目】(1)如图1,AB∥CD,∠PAB=120°,∠PCD=110°,求∠APC的度数.小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答;如图3,点A、B在射线OM上,点C、D在射线ON上,AD∥BC,点P在射线OM上运动(点P与A、B、O三点不重合).
(2)当点P在线段AB上运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由;
(3)当点P在线段AB外运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由.
相关试题

