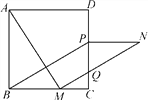
【题目】如图,在正方形ABCD中,点M是BC边上的任一点,连结AM并将线段AM绕点M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连结NP、BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连结AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
参考答案:
【答案】(1)见解析;(2)BM=MC.理由见解析
【解析】试题分析:(1)由已知条件不难证明△ABM≌△BCP,可得出AM=BP,∠BAM=∠CBP,因为∠BAM+∠AMB=90°,所以∠CBP+∠AMB=90°,所以AM⊥BP,由题意得AM⊥MN,且AM=MN,所以MN∥BP,MN=BP,故证明出四边形BMNP是平行四边形;(2)BM=MC,连接AQ,由已知条件不难证明△ABM∽△MCQ,可得![]() =
=![]() ,因为△MCQ∽△AMQ,
,因为△MCQ∽△AMQ,
所以△AMQ∽△ABM,可得![]() =
=![]() ,所以
,所以![]() =
=![]() ,所以BM=MC.
,所以BM=MC.
试题解析:
(1)证明:在正方形ABCD中,AB=BC,∠ABC=∠C.
在△ABM和△BCP中,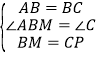 ,
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠BAM=∠CBP,
∵∠BAM+∠AMB=90°,
∴∠CBP+∠AMB=90°,
∴AM⊥BP,
∵将线段AM绕点M顺时针旋转90°得到线段MN,
∴AM⊥MN,且AM=MN,
∴MN∥BP,MN=BP,
∴四边形BMNP是平行四边形;
(2) BM=MC,理由如下:
连接AQ,
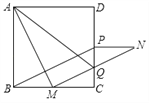
∵∠BAM+∠AMB=90°,∠AMB+∠CMQ=90°,
∴∠BAM=∠CMQ,
又∵∠B=∠C=90°,
∴△ABM∽△MCQ,
∴![]() =
=![]() ,
,
∵△MCQ∽△AMQ,
∴△AMQ∽△ABM,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BM=MC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDF;
(2)若AB=4,BC=8,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先填写表,通过观察后再回答问题:
a
……
0.0001
0.01
1
100
10000
……
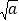
……
0.01
x
1
y
100
……
(1)表格中,x=_________,y=_________
(2)从表格中探究a与
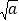 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:①已知
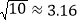 ,则
,则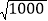 ≈___________
≈___________②已知
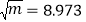 ,若
,若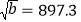 ,用含m的代数式表示b,则b=___________
,用含m的代数式表示b,则b=___________(3)试比较
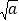 与a的大小(直接写出结果)
与a的大小(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
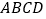 中,
中,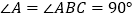 ,
,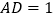 ,
,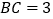 ,
,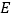 是边
是边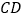 的中点,连接
的中点,连接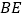 延长与
延长与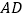 的延长线相交于点
的延长线相交于点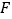 ,连接
,连接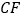 .
.(
 )求证:四边形
)求证:四边形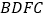 是平行四边形.
是平行四边形.(
 )已知
)已知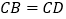 ,求四边形
,求四边形 的面积.
的面积.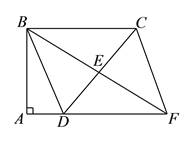
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合.三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,请直接写出
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。

求证:(1)△ADF≌△CBE
(2)EB∥DF.
相关试题

