【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起.
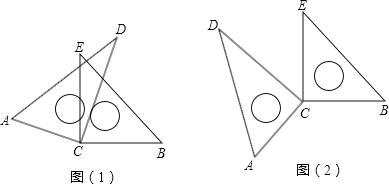
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
参考答案:
【答案】(1)∠ACE=∠BCD;(2)150°;(3)∠ECD+∠ACB=180°;(4)成立.
【解析】解:(1)∠ACE=∠BCD,理由如下:
∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD;
(2)若∠DCE=30°,∠ACD=90°,
∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°;
(3)猜想∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°;
(4)成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b是一元二次方程x2+x﹣1=0的两根,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某射击运动员在同一条件下的射击成绩记录如表:
射击次数
100
200
400
1000
“射中9环以上”的次数
78
158
321
801
“射中9环以上”的频率
0.78
0.79
0.8025
0.801
根据表中数据,估计这位射击运动员射击一次时“射中9环以上”的概率为( )
A.0.78B.0.79C.0.85D.0.80
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n=( )

A. 14 B. 15 C. 16 D. 17
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个等腰三角形的两边长分别是4cm和5cm,那么此三角形的周长是( )
A. 13cm B. 14cm C. 15cm D. 13cm或14cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等腰直角三角板放在正方形ABCD的顶点B处,且三角板中BE=EF.连AE,再作EG⊥AE且EG=AE.绕点B旋转三角板,并保证线段FG与正方形的边CD交于点H.
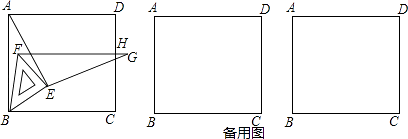
(1)求证:△ABE≌△GFE.
(2)当DH取得最小值时,求∠ABE的度数.
(3)当三角板有两个顶点在边BC上时,求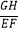 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,面积为28的平行四边形纸片ABCD中,AB=7,∠BAD=45°,按下列步骤进行裁剪和拼图.
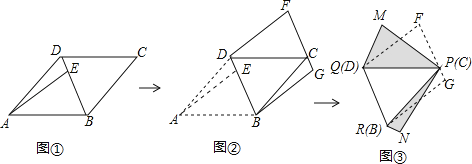
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
相关试题

