【题目】如图,在平面直角坐标系中,抛物线![]() (m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线
(m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线![]() 相交于点E,与x轴相交于点D,点P在直线
相交于点E,与x轴相交于点D,点P在直线![]() 上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
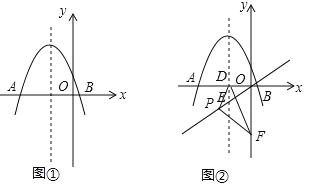
(1)如图①所示,若抛物线顶点的纵坐标为![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)求A、B两点的坐标;
(3)如图②所示,小红在探究点P的位置发现:当点P与点E重合时,∠PDF的大小为定值,进而猜想:对于直线![]() 上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
参考答案:
【答案】(1)![]() ;(2)A(﹣5,0)、B(1,0);(3)∠PDF=60°.
;(2)A(﹣5,0)、B(1,0);(3)∠PDF=60°.
【解析】
试题分析:(1)先提取公式因式将原式变形为![]() ,然后令y=0可求得函数图象与x轴的交点坐标,从而可求得点A、B的坐标,然后依据抛物线的对称性可得到抛物线的对称轴为x=﹣2,故此可知当x=﹣2时,y=
,然后令y=0可求得函数图象与x轴的交点坐标,从而可求得点A、B的坐标,然后依据抛物线的对称性可得到抛物线的对称轴为x=﹣2,故此可知当x=﹣2时,y=![]() ,于是可求得m的值;
,于是可求得m的值;
(2)由(1)的可知点A、B的坐标;
(3)先由一次函数的解析式得到∠PBF的度数,然后再由PD⊥PF,FO⊥OD,证明点O、D、P、F共圆,最后依据圆周角定理可证明∠PDF=60°.
试题解析:(1)∵![]() ,∴
,∴![]() =m(x+5)(x﹣1).令y=0得:m(x+5)(x﹣1)=0,∵m≠0,∴x=﹣5或x=1,∴A(﹣5,0)、B(1,0),∴抛物线的对称轴为x=﹣2.∵抛物线的顶点坐标为为
=m(x+5)(x﹣1).令y=0得:m(x+5)(x﹣1)=0,∵m≠0,∴x=﹣5或x=1,∴A(﹣5,0)、B(1,0),∴抛物线的对称轴为x=﹣2.∵抛物线的顶点坐标为为![]() ,∴﹣9m=
,∴﹣9m=![]() ,∴m=
,∴m=![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ;
;
(2)由(1)可知:A(﹣5,0)、B(1,0);
(3)∠PDF=60°.理由如下:
如图所示,∵OP的解析式为![]() ,∴∠AOP=30°,∴∠PBF=60°
,∴∠AOP=30°,∴∠PBF=60°
∵PD⊥PF,FO⊥OD,∴∠DPF=∠FOD=90°,∴∠DPF+∠FOD=180°,∴点O、D、P、F共圆,∴∠PDF=∠PBF,∴∠PDF=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:5,15,75,45,25,75,45,35,45,35,那么40是这一组数据的( )
A. 平均数但不是中位数 B. 平均数也是中位数
C. 众数 D. 中位数但不是平均数
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2a2)2a,正确的是( )
A. 2a5 B. ﹣4a5 C. 4a5 D. 4a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示136000,其结果是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为
 米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
-
科目: 来源: 题型:
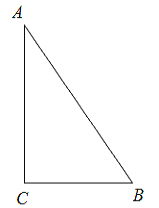
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长;
(2)问t满足什么条件时,△BCP为直角三角形;
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克,则甲种药材买了___千克.
相关试题

