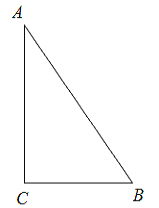
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长;
(2)问t满足什么条件时,△BCP为直角三角形;
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分.
参考答案:
【答案】(1)7+![]() ;(2)0<t≤4或t=
;(2)0<t≤4或t=![]() ;(3)t=2,t=6.
;(3)t=2,t=6.
【解析】试题分析:(1)、根据题意得出CP的长度,然后根据勾股定理得出BP的长度,从而得出△ABP的周长;(2)、根据直角三角形的性质得出t的取值范围;(3)、当P点在AC上,Q在AB上,则PC=t,BQ=2t﹣3,根据周长相等得出t的值;当P点在AB上,Q在AC上,则AC=t﹣4,AQ=2t﹣8,根据周长相等得出t的值.
试题解析:(1)、由∠C=90°,AB=5cm,BC=3cm,
∴AC=4,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm, ∴出发2秒后,则CP=2,
∵∠C=90°,∴PB=![]() , ∴△ABP的周长为:AP+PB+AB=
, ∴△ABP的周长为:AP+PB+AB=![]()
(2)、![]()
![]()
(3)、当P点在AC上,Q在AB上,则PC=t,BQ=2t﹣3,
∵直线PQ把△ABC的周长分成相等的两部分, ∴t+2t﹣3=6, ∴t=2;
当P点在AB上,Q在AC上,则AC=t﹣4,AQ=2t﹣8,
∵直线PQ把△ABC的周长分成相等的两部分, ∴t﹣4+2t﹣8=6, ∴t=6,
∴当t为2或6秒时,直线PQ把△ABC的周长分成相等的两部分
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示136000,其结果是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
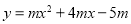 (m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线
(m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线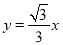 相交于点E,与x轴相交于点D,点P在直线
相交于点E,与x轴相交于点D,点P在直线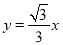 上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.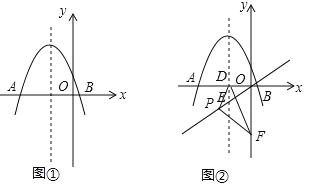
(1)如图①所示,若抛物线顶点的纵坐标为
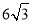 ,求抛物线的解析式;
,求抛物线的解析式;(2)求A、B两点的坐标;
(3)如图②所示,小红在探究点P的位置发现:当点P与点E重合时,∠PDF的大小为定值,进而猜想:对于直线
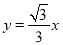 上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为
 米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克,则甲种药材买了___千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】沿着一条公路栽树,第一棵栽在路的始端,以后每隔50米栽一棵,要求路的末端栽一棵,这样,缺少21棵树;如果每隔55米栽一棵,要求在路的末端栽一棵,这样,只缺少一棵树.求树的棵数和这条公路的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,
 = 。
= 。
相关试题

