【题目】如图,正方形ABCD中,P、Q分别是边AB、BC上的两个动点,P、Q同时分别从A、B出发,点P沿AB向B运动;点Q沿BC向C运动,速度都是1个单位长度/秒.运动时间为t秒. 
(1)连结AQ、DP相交于点F,求证:AQ⊥DP;
(2)当正方形边长为4,而t=3时,求tan∠QDF的值.
参考答案:
【答案】
(1)解:在正方形ABCD中,
∵AB=AD,∠BAD=∠B=90°,
由题意得:AP=BQ,
在△ADP与△ABQ中,  ,
,
∴△ADP≌△ABQ,
∴∠BAQ=∠ADP,
∵∠PAF+∠DAF=90°,
∴∠DAF+∠ADF=90°,
∴∠AFD=90°,
∴AQ⊥DP
(2)解:∵正方形边长为4,而t=3时,
∴AD=AB=4,AP=BQ=3,
∴PD=AQ=5,
∵∠PAF=∠ADP,∠AFP=∠PAD=90°,
∴△APF∽△ADP,
∴ ![]() ,
,
∴PF= ![]() ,
,
∴DF= ![]() ,
,
∵∠AFP=∠AFD=90°,
∴△APF∽△ADF,
∴ ![]() ,
,
∴AF= ![]() ,
,
∴FQ= ![]() ,
,
∴tan∠QDF= ![]() =
= ![]()
【解析】(1)根据正方形的性质得到AB=AD,∠BAD=∠B=90°,推出△ADP≌△ABQ,由全等三角形的性质得到∠BAQ=∠ADP,根据余角的性质即可得到结论;(2)根据勾股定理得到PD=AQ=5,推出△APF∽△ADP,根据相似三角形的性质得到 ![]() ,求得PF=
,求得PF= ![]() ,得到DF=
,得到DF= ![]() ,同理得到AF=
,同理得到AF= ![]() ,求得FQ=
,求得FQ= ![]() ,根据三角函数的定义即可得到结论.
,根据三角函数的定义即可得到结论.
【考点精析】掌握正方形的性质和相似三角形的判定与性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
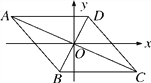
查看答案和解析>>【题目】如图,已知点A(-4,2),B(-1,-2),□ABCD的对角线交于坐标原点O.
(1)请写出点C,D的坐标;
(2)指出从线段AB到线段DC的变换过程;
(3)求□ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
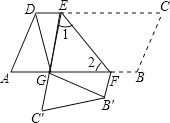
求证:(1)∠1=∠2;
(2)DG=B′G.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:
下面是一个有关平行四边形和等边三角形的小实验,请根据实验解答问题:
已知在□ABCD中,∠ABC=120°,点D又是等边三角形DEF的一个顶点,DE与AB相交于点M,DF与BC相交于点N(不包括线段的端点).
(1)初步尝试:
如图①,若AB=BC,求证:BD=BM+BN;
(2)探究发现:
如图②,若BC=2AB,过点D作DH⊥BC于点H,求证:∠BDC=90°.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,3).且点A的坐标为(﹣1,0),点B的坐标为(3,0),点P是抛物线上第一象限内的一个点.

(1)求抛物线的函数表达式;
(2)连PO、PB,如果把△POB沿OB翻转,所得四边形POP′B恰为菱形,那么在抛物线的对称轴上是否存在点Q,使△QAB与△POB相似?若存在求出点Q的坐标;若不存在,说明理由;
(3)若(2)中点Q存在,指出△QAB与△POB是否位似?若位似,请直接写出其位似中心的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】解分式方程:
(1)

(2)
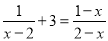 .
.
相关试题

