【题目】为满足市场需求,某超市在“圣诞节”来临前夕,购进一种品牌巧克力,每盒进价是![]() 元.超市规定每盒售价不得少于
元.超市规定每盒售价不得少于![]() 元,根据以往销售经验发现;当售价定为每盒
元,根据以往销售经验发现;当售价定为每盒![]() 元时,每天可以卖出
元时,每天可以卖出![]() 盒,每盒售价提高
盒,每盒售价提高![]() 元,每天要少卖出
元,每天要少卖出![]() 盒.
盒.
(![]() )试求出每天的销售量
)试求出每天的销售量![]() (盒)与每盒售价
(盒)与每盒售价![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(![]() )当每盒售价定为多少元时,每天销售的利润
)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
(![]() )为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于
)为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于![]() 元.如果超市想要每天获得不低于
元.如果超市想要每天获得不低于![]() 元的利润,那么超市每天至少销售巧克力多少盒?
元的利润,那么超市每天至少销售巧克力多少盒?
参考答案:
【答案】(1)![]() ;(2)当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;(3)440.
;(2)当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;(3)440.
【解析】试题分析:(1)根据“当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒”即可得出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)根据“利润=1盒巧克力所获得的利润×销售量”列式整理,再根据二次函数的最值问题解答即可;
(3)先由(2)中所求得的P与x的函数关系式,根据“这种巧克力的每盒售价不得高于58元,且每天销售巧克力的利润不低于6000元”,求出x的取值范围,再根据(1)中所求得的销售量y(盒)与每盒售价x(元)之间的函数关系式即可求解.
试题解析:解:(1)由题意得:y=700﹣20(x﹣45)=﹣20x+1600;
(2)P=(x﹣40)(﹣20x+1600)=﹣20x2+2400x﹣64000=﹣20(x﹣60)2+8000.∵x≥45,a=﹣20<0,∴当x=60时,P最大值=8000元,即当每盒售价定为60元时,每天销售的利润P最大,最大利润是8000元;
(3)由题意得:﹣20(x﹣60)2+8000=6000,解得x1=50,x2=70.
∵抛物线P=﹣20(x﹣60)2+8000的开口向下,∴当50≤x≤70时,每天销售巧克力的利润不低于6000元的利润.
又∵x≤58,∴50≤x≤58.
∵在y=﹣20x+1600中,k=﹣20<0,∴y随x的增大而减小,∴当x=58时,y最小值=﹣20×58+1600=440,即超市每天至少销售巧克力440盒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.
(1)在实验中他们共做了50次试验,试验结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
10
9
6
9
8
8
填空:此次实验中,“1点朝上”的频率是 ;
② 小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?
(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表:
试验总次数
100
200
500
1000
2000
5000
10000
1点朝上的次数
18
34
82
168
330
835
1660
1点朝上的频率
0.180
0.170
0.164
0.168
0.165
0.167
0.166
“1点朝上”的概率的估计值是 .
-
科目: 来源: 题型:
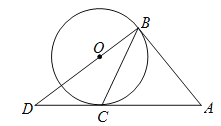
查看答案和解析>>【题目】如图,已知
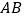 、
、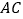 与⊙
与⊙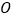 相切于点
相切于点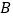 、
、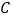 ,连接
,连接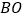 并延长交
并延长交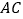 于点
于点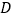 .若
.若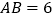 ,
,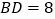 .
.
(
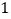 )求⊙
)求⊙ 的半径
的半径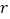 .
.(
 )求
)求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=15cm,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立即改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
(1)若点P点Q同时出发,且当点P与点Q重合时,求t的值.
(2)若点P点Q同时出发,在P与Q相遇前,若点P是线段AQ的三等分点时,求t的值.
(3)若点P点Q同时出发,Q点与P点相遇后仍然继续往A点的方向运动到A点后再返回,求整个运动过程中PQ为6cm时t的值 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
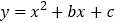 的图像与
的图像与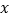 轴交于
轴交于 、
、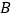 两点,与
两点,与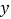 轴交于
轴交于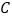 点,点
点,点 是抛物线顶点,点
是抛物线顶点,点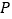 是直线
是直线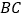 下方的抛物线上一动点.
下方的抛物线上一动点.(
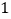 )这个二次函数的表达式为____________.
)这个二次函数的表达式为____________.(
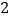 )设直线
)设直线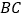 的解析式为
的解析式为 ,则不等式
,则不等式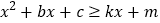 的解集为___________.
的解集为___________.(
 )连结
)连结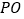 、
、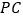 ,并把
,并把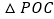 沿
沿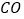 翻折,得到四边形
翻折,得到四边形 ,那么是否存在点
,那么是否存在点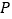 ,使四边形
,使四边形 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点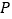 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(
 )当四边形
)当四边形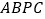 的面积最大时,求出此时
的面积最大时,求出此时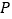 点的坐标和四边形
点的坐标和四边形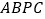 的最大面积.
的最大面积.(
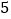 )若把条件“点
)若把条件“点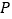 是直线
是直线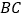 下方的抛物线上一动点.”改为“点
下方的抛物线上一动点.”改为“点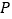 是抛物线上的任一动点”,其它条件不变,当以
是抛物线上的任一动点”,其它条件不变,当以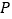 、
、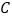 、
、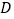 、
、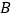 为顶点的四边形为梯形时,直接写出点
为顶点的四边形为梯形时,直接写出点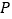 的坐标.
的坐标.
-
科目: 来源: 题型:
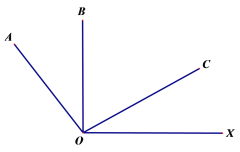
查看答案和解析>>【题目】如图:已知OB⊥OX,OA⊥OC,∠COX=40°,若射线OA绕O点以每秒30°的速度顺时针旋转,射线OC绕O点每秒10°的速度逆时针旋转, 两条射线同时旋转,当一条射线与射线OX重合时,停止运动.
(1)开始旋转前,∠AOB=______________
(2)当OA与OC的夹角是10°时,求旋转的时间.
(3)若射线OB也绕O点以每秒20°的速度顺时针旋转,三条射线同时旋转,当一条射线与射线OX重合时,停止运动.当三条射线中其中一条射线是另外两条射线夹角的角平分线时,求旋转的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题(说明:测试成绩在总人数的前30%考生为A等级,前30%至前70%为B等级,前70%至前90%为C等级,90%以后为D等级)

(1)抽取了 名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 ;
(4)若测试成绩在总人数的前90%为合格,该校初二年级有800名学生,求全年级生物合格的学生共约多少人.
相关试题

