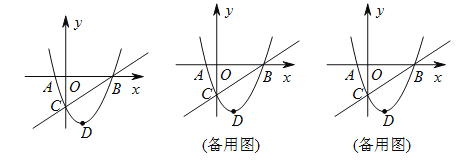
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线顶点,点
是抛物线顶点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
(![]() )这个二次函数的表达式为____________.
)这个二次函数的表达式为____________.
(![]() )设直线
)设直线![]() 的解析式为
的解析式为![]() ,则不等式
,则不等式![]() 的解集为___________.
的解集为___________.
(![]() )连结
)连结![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点
,那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(![]() )当四边形
)当四边形![]() 的面积最大时,求出此时
的面积最大时,求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
(![]() )若把条件“点
)若把条件“点![]() 是直线
是直线![]() 下方的抛物线上一动点.”改为“点
下方的抛物线上一动点.”改为“点![]() 是抛物线上的任一动点”,其它条件不变,当以
是抛物线上的任一动点”,其它条件不变,当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为梯形时,直接写出点
为顶点的四边形为梯形时,直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ;(2)x≤0或x≥3;(3)
;(2)x≤0或x≥3;(3)![]() ;(4)当P(
;(4)当P(![]() ,
,![]() )时,S四边形ABPC最大
)时,S四边形ABPC最大![]() ;(5)点P的坐标为(-2,5),(2,-3)或(4,5).
;(5)点P的坐标为(-2,5),(2,-3)或(4,5).
【解析】试题分析:(1)直接设成顶点式即可得出抛物线解析式;
(2)先确定出点B,C坐标,再根据图象直接写出范围;
(3)利用菱形的性质得出PO=PC即可得出点P的纵坐标,代入抛物线解析式即可得出结论;
(4)先利用坐标系中几何图形的面积的计算方法建立函数关系式即可求出面积的最大值;
(5)先求出直线BC,BC,CD的解析式,分三种情况利用梯形的性质,一组对边平行即可得出直线DP1,CP2,BP3的解析式,分别联立抛物线的解析式建立方程组求解即可.
试题解析:解:(1)∵点D(1,﹣4)是抛物线y=x2+bx+c的顶点,∴y=(x﹣1)2﹣4=x2﹣2x﹣3.故答案为:y=x2﹣2x﹣3;
(2)令x=0,∴y=﹣3,∴C(0,﹣3),令y=0,∴x2﹣2x﹣3=0,∴x=﹣1或x=3,∴A(﹣1,0),B(3,0),∴不等式x2+bx+c≥kx+m的解集为x<0或>3.故答案为:x<0或>3;
(3)如图1.∵四边形POP′C为菱形,∴PO=PC.∵C(0,﹣3),∴点P的纵坐标为﹣![]() .∵P在抛物线y=x2﹣2x﹣3上,∴﹣
.∵P在抛物线y=x2﹣2x﹣3上,∴﹣![]() =x2﹣2x﹣3,∴x=
=x2﹣2x﹣3,∴x=![]() 或x=
或x=![]() (舍),∴P(
(舍),∴P(![]() .﹣
.﹣![]() );
);
(4)如图2,由(1)知,B(3,0),C(0,﹣3),∴直线BC的解析式为y=x﹣3,过点P作PE∥y轴交BC于E,设P(m,m2﹣2m﹣3),(0<m<3)
∴E(m,m﹣3),∴PE=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m.∵A(﹣1,0),B(3,0),C(0,﹣3),∴S四边形ABPC=S△ABC+S△PCE+S△PBE=![]() ABOC+
ABOC+![]() PE|xP|+
PE|xP|+![]() PE|xB﹣xP|
PE|xB﹣xP|
=![]() ABOC+
ABOC+![]() PE(|xP|+|xB﹣xP|)=
PE(|xP|+|xB﹣xP|)=![]() ×4×3+
×4×3+![]() (﹣m2+3m)×(m+3﹣m)
(﹣m2+3m)×(m+3﹣m)
=6+![]() ×(﹣m2+3m)=﹣
×(﹣m2+3m)=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]()
当m=![]() 时,S四边形ABPC最大=
时,S四边形ABPC最大=![]() .
.
当m=![]() 时,m2﹣2m﹣3=
时,m2﹣2m﹣3=![]() ,∴P(
,∴P(![]() ,
,![]() ).
).
(5)如图,由(1)知,B(3,0),C(0,﹣3),D(1,﹣4),∴直线BC的解析式为y=x﹣3,直线BD的解析式为y=2x﹣6,直线CD的解析式为y=﹣x﹣3.∵以P、C、D、B为顶点的四边形为梯形.∵抛物线的解析式为y=x2﹣2x﹣3①;
①当DP1∥BC时,∴直线DP1的解析式为y=x﹣5②,联立①②解得,点P1(2,﹣3),[另一个点为(1,﹣4)和点D重合,舍去]
②当CP2∥BD时,∴直线CP2的解析式为y=2x﹣3③,联立①③解得点P2(4,5)
③当BP3∥CD时,∴直线BP3∥CD的解析式为y=﹣x+3④,联立①④解得点P3(﹣2,5).
综上所述:以P、C、D、B为顶点的四边形为梯形时,点P的坐标为(﹣2,5)、(2,﹣3)或(4,5).

-
科目: 来源: 题型:
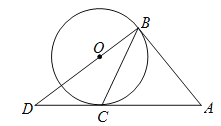
查看答案和解析>>【题目】如图,已知
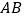 、
、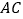 与⊙
与⊙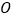 相切于点
相切于点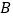 、
、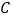 ,连接
,连接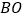 并延长交
并延长交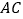 于点
于点 .若
.若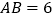 ,
,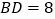 .
.
(
 )求⊙
)求⊙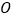 的半径
的半径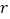 .
.(
 )求
)求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=15cm,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立即改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
(1)若点P点Q同时出发,且当点P与点Q重合时,求t的值.
(2)若点P点Q同时出发,在P与Q相遇前,若点P是线段AQ的三等分点时,求t的值.
(3)若点P点Q同时出发,Q点与P点相遇后仍然继续往A点的方向运动到A点后再返回,求整个运动过程中PQ为6cm时t的值 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,某超市在“圣诞节”来临前夕,购进一种品牌巧克力,每盒进价是
 元.超市规定每盒售价不得少于
元.超市规定每盒售价不得少于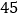 元,根据以往销售经验发现;当售价定为每盒
元,根据以往销售经验发现;当售价定为每盒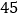 元时,每天可以卖出
元时,每天可以卖出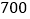 盒,每盒售价提高
盒,每盒售价提高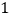 元,每天要少卖出
元,每天要少卖出 盒.
盒.(
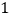 )试求出每天的销售量
)试求出每天的销售量 (盒)与每盒售价
(盒)与每盒售价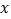 (元)之间的函数关系式.
(元)之间的函数关系式.(
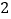 )当每盒售价定为多少元时,每天销售的利润
)当每盒售价定为多少元时,每天销售的利润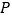 (元)最大?最大利润是多少?
(元)最大?最大利润是多少?(
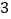 )为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于
)为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于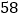 元.如果超市想要每天获得不低于
元.如果超市想要每天获得不低于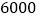 元的利润,那么超市每天至少销售巧克力多少盒?
元的利润,那么超市每天至少销售巧克力多少盒? -
科目: 来源: 题型:
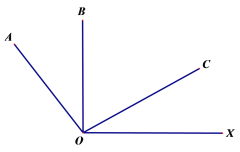
查看答案和解析>>【题目】如图:已知OB⊥OX,OA⊥OC,∠COX=40°,若射线OA绕O点以每秒30°的速度顺时针旋转,射线OC绕O点每秒10°的速度逆时针旋转, 两条射线同时旋转,当一条射线与射线OX重合时,停止运动.
(1)开始旋转前,∠AOB=______________
(2)当OA与OC的夹角是10°时,求旋转的时间.
(3)若射线OB也绕O点以每秒20°的速度顺时针旋转,三条射线同时旋转,当一条射线与射线OX重合时,停止运动.当三条射线中其中一条射线是另外两条射线夹角的角平分线时,求旋转的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题(说明:测试成绩在总人数的前30%考生为A等级,前30%至前70%为B等级,前70%至前90%为C等级,90%以后为D等级)

(1)抽取了 名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 ;
(4)若测试成绩在总人数的前90%为合格,该校初二年级有800名学生,求全年级生物合格的学生共约多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的边AB长为4cm,DE平分∠ADC,若∠B=80°,∠DAE=50°,求平行四边形ABCD的周长?

相关试题

