【题目】如图,线段AB=15cm,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立即改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
(1)若点P点Q同时出发,且当点P与点Q重合时,求t的值.
(2)若点P点Q同时出发,在P与Q相遇前,若点P是线段AQ的三等分点时,求t的值.
(3)若点P点Q同时出发,Q点与P点相遇后仍然继续往A点的方向运动到A点后再返回,求整个运动过程中PQ为6cm时t的值 .
![]()
参考答案:
【答案】(1)t=5(秒);(2)t=3或t=30/7;(3)当PQ=6cm时,t=3或t=7或t=9或t=21
【解析】
(1)根据相遇时,两点共同走了15cm列方程解答即可;
(2)分两种情况列方程求解即可:①当AP= ![]() AQ时,②当AP=
AQ时,②当AP= ![]() AQ时;
AQ时;
(3)分四种情况列方程求解即可:①相遇前PQ=6,②相遇后Q未到达A点前PQ=6,③相遇后Q到达A后返回未追上P时PQ=6,④相遇后Q到达A后返回追上P时PQ=6.
解: (1)∵t+2t=15 ,
则t=5(秒);
(2)①当AP= ![]() AQ时,即t=
AQ时,即t=![]() (15-2t),
(15-2t),
∴t=3;
②当AP= ![]() AQ时,即t=
AQ时,即t=![]() (15-2t),
(15-2t),
∴t=![]() ,
,
即当P点是AQ的三等分点时t=3或t=![]() ;
;
(3)①相遇前PQ=6,即15-t-2t=6,
∴t=3![]()
②相遇后Q未到达A点前PQ=6,即t+2t=15+6
∴t=7,
③相遇后Q到达A后返回未追上P时PQ=6,即2t-15+6=t,
∴t=9,
④相遇后Q到达A后返回追上P时PQ=6,即2t-15-t=6,
∴t=21,
综上所述当PQ=6cm时,t=3或t=7或t=9或t=21.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图像经过点
的图像经过点 .
.(
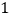 )求该二次函数的关系式.
)求该二次函数的关系式.(
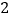 )证明:无论
)证明:无论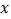 取何值,函数值
取何值,函数值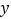 总不等于
总不等于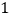 .
.(
 )将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
)将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点. -
科目: 来源: 题型:
查看答案和解析>>【题目】小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.
(1)在实验中他们共做了50次试验,试验结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
10
9
6
9
8
8
填空:此次实验中,“1点朝上”的频率是 ;
② 小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?
(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表:
试验总次数
100
200
500
1000
2000
5000
10000
1点朝上的次数
18
34
82
168
330
835
1660
1点朝上的频率
0.180
0.170
0.164
0.168
0.165
0.167
0.166
“1点朝上”的概率的估计值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
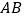 、
、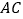 与⊙
与⊙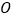 相切于点
相切于点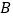 、
、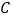 ,连接
,连接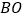 并延长交
并延长交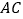 于点
于点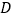 .若
.若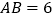 ,
,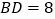 .
.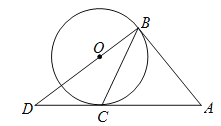
(
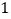 )求⊙
)求⊙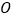 的半径
的半径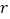 .
.(
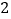 )求
)求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,某超市在“圣诞节”来临前夕,购进一种品牌巧克力,每盒进价是
 元.超市规定每盒售价不得少于
元.超市规定每盒售价不得少于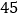 元,根据以往销售经验发现;当售价定为每盒
元,根据以往销售经验发现;当售价定为每盒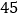 元时,每天可以卖出
元时,每天可以卖出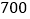 盒,每盒售价提高
盒,每盒售价提高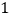 元,每天要少卖出
元,每天要少卖出 盒.
盒.(
 )试求出每天的销售量
)试求出每天的销售量 (盒)与每盒售价
(盒)与每盒售价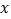 (元)之间的函数关系式.
(元)之间的函数关系式.(
 )当每盒售价定为多少元时,每天销售的利润
)当每盒售价定为多少元时,每天销售的利润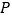 (元)最大?最大利润是多少?
(元)最大?最大利润是多少?(
 )为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于
)为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于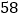 元.如果超市想要每天获得不低于
元.如果超市想要每天获得不低于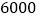 元的利润,那么超市每天至少销售巧克力多少盒?
元的利润,那么超市每天至少销售巧克力多少盒? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
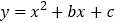 的图像与
的图像与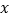 轴交于
轴交于 、
、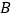 两点,与
两点,与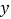 轴交于
轴交于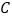 点,点
点,点 是抛物线顶点,点
是抛物线顶点,点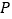 是直线
是直线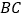 下方的抛物线上一动点.
下方的抛物线上一动点.(
 )这个二次函数的表达式为____________.
)这个二次函数的表达式为____________.(
 )设直线
)设直线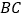 的解析式为
的解析式为 ,则不等式
,则不等式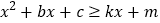 的解集为___________.
的解集为___________.(
 )连结
)连结 、
、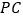 ,并把
,并把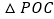 沿
沿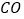 翻折,得到四边形
翻折,得到四边形 ,那么是否存在点
,那么是否存在点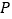 ,使四边形
,使四边形 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点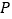 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(
 )当四边形
)当四边形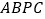 的面积最大时,求出此时
的面积最大时,求出此时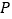 点的坐标和四边形
点的坐标和四边形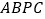 的最大面积.
的最大面积.(
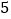 )若把条件“点
)若把条件“点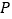 是直线
是直线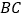 下方的抛物线上一动点.”改为“点
下方的抛物线上一动点.”改为“点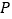 是抛物线上的任一动点”,其它条件不变,当以
是抛物线上的任一动点”,其它条件不变,当以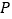 、
、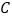 、
、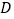 、
、 为顶点的四边形为梯形时,直接写出点
为顶点的四边形为梯形时,直接写出点 的坐标.
的坐标.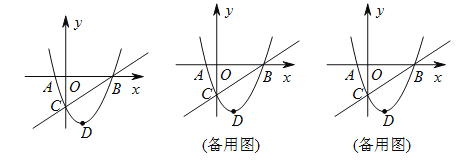
-
科目: 来源: 题型:
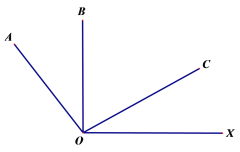
查看答案和解析>>【题目】如图:已知OB⊥OX,OA⊥OC,∠COX=40°,若射线OA绕O点以每秒30°的速度顺时针旋转,射线OC绕O点每秒10°的速度逆时针旋转, 两条射线同时旋转,当一条射线与射线OX重合时,停止运动.
(1)开始旋转前,∠AOB=______________
(2)当OA与OC的夹角是10°时,求旋转的时间.
(3)若射线OB也绕O点以每秒20°的速度顺时针旋转,三条射线同时旋转,当一条射线与射线OX重合时,停止运动.当三条射线中其中一条射线是另外两条射线夹角的角平分线时,求旋转的时间.
相关试题

